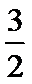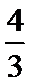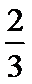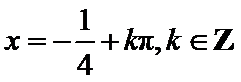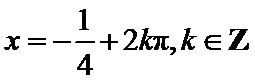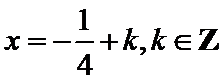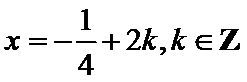由y=Asin（ωx+φ）的部分图象确定其解析式
共39题

· 由y=Asin（ωx+φ）的部分图象确定其解析式

由y=Asin（ωx+φ）的部分图象确定其解析式
共39题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

1.已知ω>0,|φ|<,函数f（x）=sin（ωx+φ）的部分图象如图所示.则·（）=（　　）.

正确答案

解析

由图可知,T=-=,∴T==π,∴ω=2,

∴f(x)=sin(2x+φ),又×2+φ=2kπ+π(k∈Z),

∴φ=2kπ+(k∈Z),又|φ|<,∴φ=,

∴f(x)=sin(2x+),

令x=0,得M(0,),令y=-,得N(π,-),

∴·(+)=(-)·(+)=||2-||2=()2+-()2=.

知识点

由y=Asin（ωx+φ）的部分图象确定其解析式平面向量数量积的运算

题型：单选题

单选题 · 5 分

4. 函数f(x)＝2sin(ωx＋φ)的部分图象如图所示，则ω，φ的值分别是(　　)

A2，

B2，

C4，

D4，

正确答案

考查方向

本题主要考查了由三角函数的图象和性质求解析式,在近几年的各省高考题出现的频率较高，常与三角恒等变形公式，函数单调性、周期性、对称型、奇偶性等知识点交汇命题。

解题思路

１、由图可知，进出求出；

２、把点代入得，即。故选Ａ

易错点

1、本题易在对性质理解不到位没有办法求出的值。

2、本题在求上应全最值点，也易忽略题目所给的范围。

知识点

由y=Asin（ωx+φ）的部分图象确定其解析式

题型：单选题

单选题 · 3 分

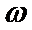
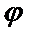
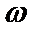
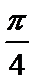
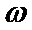
9.己知A(x1，0)，B(x2，1)在函数f(x)=2sin(x+) (>0)的图象上，|x1-x2|的最小值，则=

正确答案

解析

将点A,B代入f(x)表达式，得，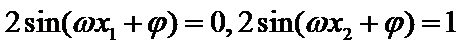

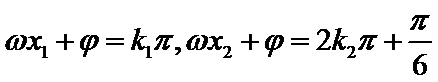
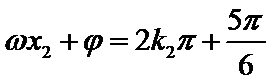
解得：（或），

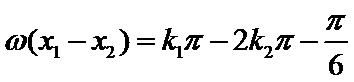
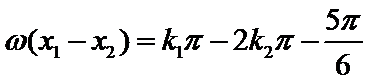
两式相减得（或），

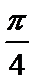
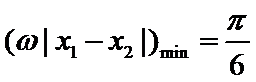
因此当|x1-x2|的最小值时，

，

所以=，故选D。

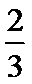
考查方向

本题主要考查了三角函数的图像及性质。

解题思路

把点A,B代入函数表达式，然后求出|x1-x2|的关系式，然后研究其最小值即可。

易错点

不能正确理解题意。

知识点

由y=Asin（ωx+φ）的部分图象确定其解析式

题型：单选题

单选题 · 5 分

7.先将函数的图像向右平移个单位长度，再作所得的图像关于y轴的对称图形，则最后函数图像的解析式为（）

正确答案

解析

向右平移函数解析式变为，然后再关于轴对称，纵坐标不变，横坐标变为相反数，所以得到，得到C答案。

考查方向

本题主要考查三角函数的图像的平移和对称翻折变换，难度中等，是高考热点之一。常常结合三角函数的单调性与最值、对称轴和对称中心等一起出题。

解题思路

先向右平移，注意一定要乘前面的系数，然后按照对称的点的坐标的关系进行关于轴对称的变换，纵坐标不变，横坐标互为相反数。

注意本题的答案还可以继续利用诱导公式进行变形，若我们在做出来的答案没有与之相同的选项的时候，就需要进一步变形。

易错点

1、左右平移的时候没有乘前面的系数；

2、图像关于轴对称不知道解析式该如何变换

知识点

函数y=Asin（ωx+φ）的图象变换由y=Asin（ωx+φ）的部分图象确定其解析式

题型：单选题

单选题 · 5 分

8.函数的部分图像如图所示，则的对称轴为（）

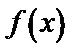
正确答案

解析

由图可知，，

故，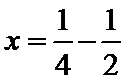

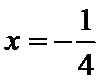
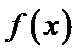
即是的一条对称轴．

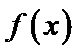
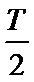
又因为每两相邻的对称轴距离均为，

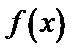
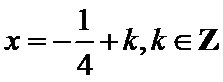
所以的对称轴为．

应选C．

考查方向

本题主要考查三角函数的图象，对称轴，周期等内容，难度不大，考查数形结合的思想方法。

解题思路

1.结合图形算出周期；

2.利用周期与对称轴之间的距离关系，得出结果，

应选C。

易错点

本题不易理解周期与对称轴之间，以及对称轴与对称轴之间的距离关系。

知识点

由y=Asin（ωx+φ）的部分图象确定其解析式

继续学习学习下一知识点

下一知识点 : y=Asin（ωx+φ）中参数的物理意义

百度题库 > 高考 > 理科数学 > 由y=Asin（ωx+φ）的部分图象确定其解析式

扫码查看完整答案与解析