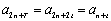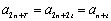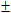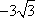- 等比数列的基本运算
- 共112题
1
题型:简答题
|
已知数列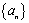
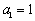
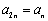
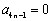
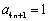
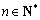
(1)求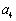
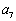
(2)是否存在正整数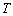
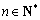
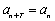
(3)设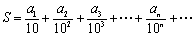
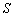
正确答案
见解析
解析
(1)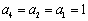
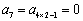
(2)假设存在正整数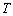
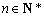
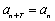
则存在无数个正整数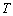
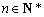
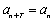
设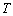
若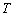
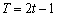
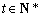
则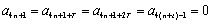
与已知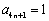
若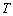
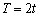
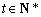
则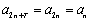
而
从而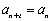
而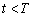
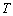
综上,不存在正整数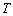
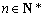
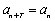
(3)若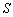
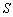
则存在正整数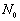
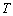
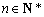
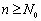
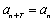
与(2)同理,设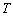
若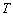
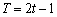
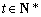
当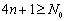
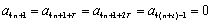
与已知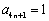
若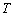
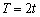
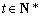
当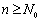
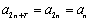
而
从而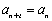
而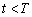
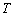
故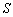
知识点
等比数列的基本运算
1
题型:
单选题
|
已知

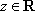
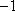

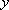

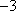
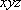
正确答案
C
解析
略
知识点
等比数列的基本运算
1
题型:
单选题
|
设等比数列






正确答案
A
解析
略
知识点
等比数列的基本运算
1
题型:填空题
|
数列




















正确答案

解析
略
知识点
等比数列的基本运算
1
题型:
单选题
|
设



正确答案
B
解析
略
知识点
等比数列的基本运算
下一知识点 : 等比数列的判断与证明
扫码查看完整答案与解析