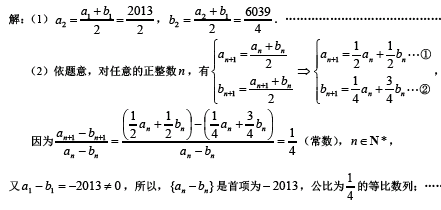
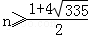- 等比数列的基本运算
- 共112题
1
题型：简答题
|
已知数列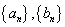
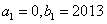
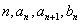
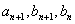
（1）求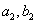
（2）证明：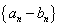
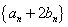
（3）是否存在唯一的正整数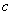
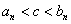
正确答案
见解析。
解析
知识点
等比数列的基本运算
1
题型：
单选题
|
已知等比数列
A0
B-2
C
D1
正确答案
C
解析
略
知识点
等比数列的基本运算等比数列的性质及应用
1
题型：
单选题
|
在等比数列
A
B
C
D
正确答案
B
解析
略
知识点
等比数列的基本运算
1
题型：简答题
|
数列{an}中，a1=3，an+1=an+cn（c是常数，n=1，2，3，…），且a1，a2，a3成公比不为1的等比数列。
（1）求c的值；
（2）求{an}的通项公式；
（3）求最小的自然数n，使an≥2013。
正确答案
见解析。
解析
（1）a1=3，a2=3+c，a3=3+3c，
∵a1，a2，a3成等比数列，∴（3+c）2=3（3+3c），
解得c=0或c=3。
当c=0时，a1=a2=a3，不符合题意舍去，故c=3。
（ 2）当n≥2时，由a2﹣a1=c，a3﹣a2=2c，…an﹣an﹣1=（n﹣1）c，
得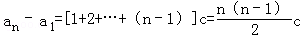
又a1=3，c=3，∴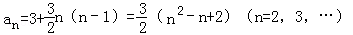
当n=1时，上式也成立，
∴
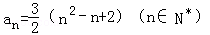
（3）由an≥2013得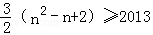
∵n∈N*，∴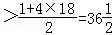
令n=37，得a37=2001＜2013，令n=38得a38=2112＞2013，
∴使an≥2013成立的最小自然数n=38。
知识点
等比数列的基本运算
1
题型：简答题
|
设正项等比数列
（1）求首项
（2）若
正确答案
见解析。
解析
（1）
∴
解得
（2）由
∴
∴
知识点
等比数列的基本运算
下一知识点 : 等比数列的判断与证明
扫码查看完整答案与解析