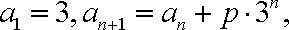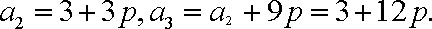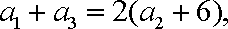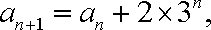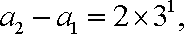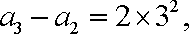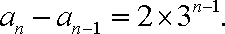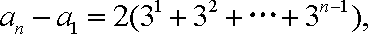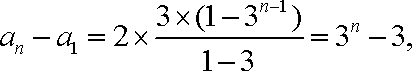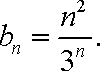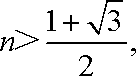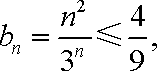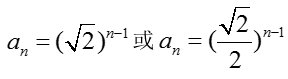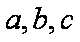- 等比数列的基本运算
- 共112题
已知常数







(1)求证:数列
(2)若对于在区间[0,1]上的任意实数




正确答案
见解析。
解析
(1)当


由




(2)由(1)知

所以
所以


记



又


知识点
已知数列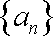
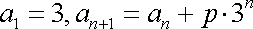
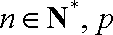
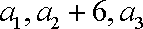
(1)求p的值及数列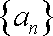
(2)设数列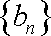
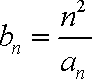
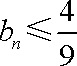
正确答案
见解析。
解析
(1)由
得
∵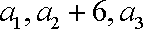
∴
即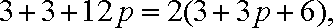
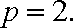
依题意知,
当
…
相加得
∴
∴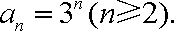
又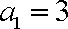
故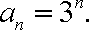
(2)证明:∵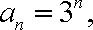
∵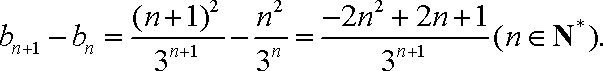
若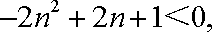
即当

又因为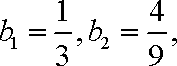
故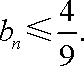
(2)法二:要证
只要证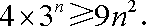
下面用数学归纳法证明:
①当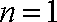
当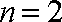
②假设当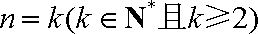

则当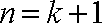
要证3×9k2≥9(k+1)2 ,
只要正3k2≥(k+1)2 ,
即证2k2-2k-1≥0.…………………………………………………………(10分)
而当k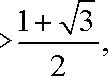
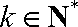

由①②可知,对任意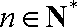
知识点
设




正确答案
解析
由

知识点
已知等比数列
正确答案
解析




知识点
已知等比数列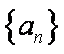
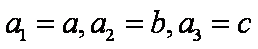
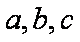
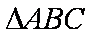
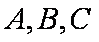
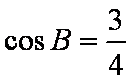
(1)求数列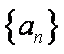
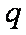
(2)设集合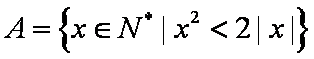
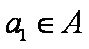
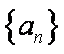
正确答案
(1)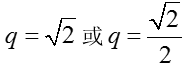
解析
解析:(1)依题意知: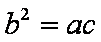
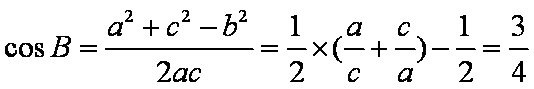
而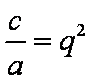
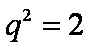
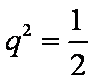
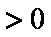
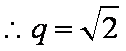
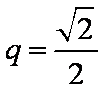
(2)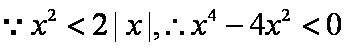
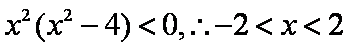
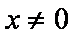
又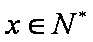
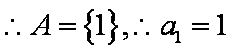
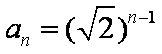

知识点
扫码查看完整答案与解析