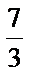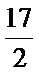- 简单空间图形的三视图
- 共140题
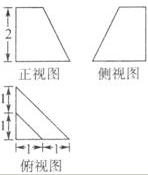
16.多面体ABCDEF(如图甲)的俯视图如图乙,己知面ADE为正三角形
(1)求多面体ABCDEF的体积;
(2)求二面角A-BF-C的余弦值.
正确答案
(1)
(2)
解析
本题属于立体几何中的基本问题,题目的难度是逐渐由易到难.
(1)分别取AB、CD的中点M、N,连接EM、EN、MN,多面体体积转化为棱柱AED-MFN的体积V1与四棱锥F-MBCN的体积V2之和。由三视图可知,AD=2,AM=DN=1,面ADE为正三角形且垂直于底面ABCD,知F点到底面的距离为



(2)取MN的中点O,BC的中点P,以OM为x轴,OP为y轴,OF为z轴建立坐标系,易知A(1,-1,0),B(1,1,0),F(0,0, 






考查方向
本题考查了立体几何中的体积和二面角的问题.属于高考中的高频考点。
解题思路
无
易错点
1、第一问中的多面体的拆分。
2、第二问中二面角的求解时要建立适当的空间直角坐标系。
知识点
10.已知某几何体的三视图如图所示,则该几何体的表面积为
正确答案
解析
该三视图所对应得空间几何体如图所示:根据台体的体积计算公式
考查方向
解题思路
1、首先根据三视图还原出原来的几何体;
2、根据空间几何体的体积计算公式选择合适的公式计算。
易错点
不能根据三视图准确地还原出原来的空间几何体而导致本题不会做。
知识点
11. 如图,是某多面体的三视图,则该多面体的体积为( )
正确答案
解析
由三视图判断知此为四棱锥
如图所示,
故
故选B选项。
考查方向
本题主要考查了由三视图还原成实物图再进行体积与表面积的计算,在近几年的各省高考题出现的频率较高,常是独立命题,求体积、表面积与棱长,也与函数结合求最值问题。
解题思路
由三视图先还原出实物的直观图(可借用正方体),再用相关公式进行求解。
易错点
1、无法由三视图还原出实物直观图。
2、公式不熟悉导致出错。
知识点
10.已知一个几何体的三视图如右图所示,则该几何体的体积为( )
正确答案
解析
根据几何体的三视图,可知,立体图形是以高为2,底面积为2的两个集合组合体,根据几何体的体积公式利用底面积乘以高求得,所以选D
考查方向
解题思路
本题考查由三视图还原几何体并且看出几何体各个部分的长度,本题解题的关键是要求体积需要求出几何体的底面面积和高,三棱锥的高是由垂直与底面的侧面的高得到,本题是一个基础题.
知识点
10.已知某几何体的三视图如图所示,则该几何体的表面积为
正确答案
解析
易知,由该几何体的三视图还原后得到原图如下:依题意知该台体ABC-A1B1C1的表面积为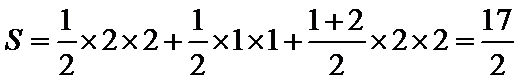
考查方向
解题思路
以三视图为载体考查空间线面位置关系的证明、求解其中一个视图的面积问题、求解几何体的表面积和体积问题等,解决此类问题的关键是能够对给出的三视图进行恰当的分析,从三视图中发现相应的位置关系与数量关系,然后在直观图中解决问.
易错点
不能由三视图还原为原图导致出错。
知识点
扫码查看完整答案与解析