- 简单空间图形的三视图
- 共140题
11.一个三棱锥的三视图是三个直角三角形，如图所示，则该三棱锥的外接球表面积是（ ）
A
B
C
D
正确答案
解析
由三视图可知几何体是地面为直角三角形，一条侧棱最值地面直角顶点的三棱锥，把它扩展为正方体，两者有相同的外接球，它的体对角线即为外接球的直径，
所以2R=
所以外接球表面积为
考查方向
解题思路
本题通过三视图考查了学生的
易错点
本题在三视图转化原图的的过程中易错。
知识点
5. 棱长为2的正方体被一平面截成两个几何体，其中一个几何体的三视图如图所示，那么该几何体的体积是（ ）
A
B4
C
D3
正确答案
解析
根据三视图将几何体放到正方体中，发现原几何体是由图中菱形的平面截得下边的部分。
由图知，该几何体的体积是正方体体积的一半，所以其体积为
考查方向
解题思路
1、将几何体放到长方体中考虑；
2、得到原来的几何体后求出其体积即可。
易错点
1.无法根据三视图还原成直观图；
2.不会计算得到几何体的体积。
知识点
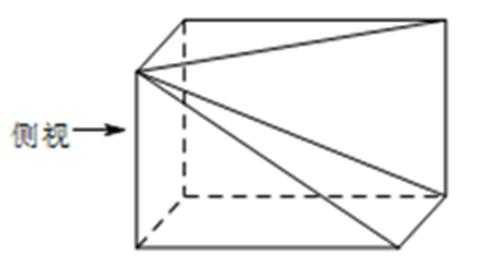
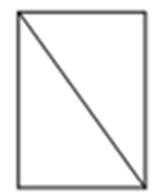
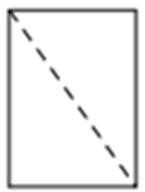
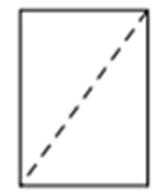
5．将长方体截去一个四棱锥，得到的几何体如图所示，则该几何体的侧视图为（ ）
A
B
C
D
正确答案
解析
据图可知侧视图是一个矩形，而且右边中间的一条棱是看不到的，所以要画成虚线，从而排除A、B选项，又可以据图知道虚线是从右上角到左下角，所以选D选项。
考查方向
解题思路
根据“长对正、高平齐、宽相等”的原则画出三视图，另外还需注意“看得见的画成实线，看不见的画成虚线”。
易错点
不能根据准确地想象中间棱的走向而导致本题做错。
知识点
11.如图，网格纸上小正方形的边长为1，粗线画出的是某个四面体的三视图，则该四面体的表面积为
A
B
C
D
正确答案
解析
由俯视图为三角形，及正视图和侧视图均为直角三角形，可知原几何体是有一侧棱与底面垂直的三棱锥，垂直于底面的侧棱长为4，另两侧棱长分别为
考查方向
解题思路
1、由正视图和侧视图均为直角三角形，可知一侧棱与底面垂直；
2、结合俯视图，得几何体为三棱锥。
易错点
无法正确还原几何体，看不到是一个倒置的三棱锥。
知识点
11．如图，网格纸上小正方形的边长为1，粗实线及粗虚线画出的是某多面体的三视图，则该多面体外接球的表面积为( )
A
B
C
D
正确答案
解析
将该几何体的三视图放到正方体中考虑，得到该几何体为四棱锥S-ABCD，其中底面为长方形，长为
考查方向
本题主要考查由三视图还原直观图、球的切接等知识，意在考查考生空间想象能力、运算求解能力等，对考生的要求很高。
解题思路
1.先根据题中给出的三视图确定该几何体的直观图为四棱锥；
2.确定四棱锥外接球的球心在的位置，然后建立方程组求出R即可。
易错点
1.无法根据三视图还原成原来的几何体；
2.无法确定外接球的球心所在位置，导致一点思路也没有。
知识点
扫码查看完整答案与解析