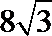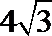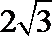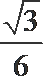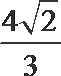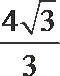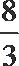- 简单空间图形的三视图
- 共140题
4．若一个正三棱柱的正视图如图所示,则其侧视图的面积等于 （ ）
A
B2
C
D6
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
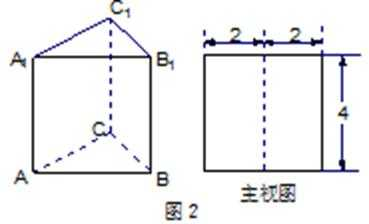
3．如图2，正三棱柱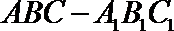
A
B
C
D16
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
6．一个几何体的三视图如图所示，这个几何体的体积是（ ）
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
18．四棱锥的正视图和俯视图如图，其中俯视图是直角梯形．
（I ）若正视图是等边三角形，F为AC的中点，当点M在棱AD上移动时，是否总有BF丄CM，请说明理由；
（II）若平面ABC与平面ADE所成的锐二面角为45°，求直线AD与平面ABE所成角的正弦值。
正确答案
（I）
若正视图是等边三角形，F为AC的中点，当点M在棱AD上移动时，总有BF丄CM．
取BC中点O，连接AO，
由俯视图可知，AO⊥面BCDE，
取DE中点H，连接OH，OH⊥BC
以OC、OH、OA分别为x，y，z轴，建立空间直角坐标系O﹣xyz，设A（0，0，
∴F（
设M（x，2x，
∴
∴
∴BF丄CM．
（II）D（1，2，0），设A（0，0，a）（a＞0），
∴
设平面ADE的法向量为
∴
∴
∴可取
∵平面ABC的法向量为
∴
∵平面ABC与平面ADE所成的锐二面角为45°，
∴
设平面ABE的法向量为
∵
∴
∴
∴可取
∴
∴直线AD与平面ABE所成角的正弦值为
解析
解析已在路上飞奔，马上就到！
知识点
5.如图，一个简单几何体的三视图其主视图与俯视图分别是边长2的正三角形和正方形，则其体积是（ ）
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
4.一个三棱锥的三视图如图所示，则该棱锥的体积等于（ ）
A
B8
C4
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
12. 已知某几何体的三视图如图所示，则该几何体的体积是__________。
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
3．如图是一正方体被过棱的中点M、N和顶点A、D、C1的两个截面截去两个角后所得
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
7．已知某几何体的三视图如图所示，则该几何体的体积等于（ ）
A
B
C
D60
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
9.如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,以该多面体的各条棱中最长的棱为标准截取8根等长的铁丝接成如图的四棱锥形骨架,把一个皮球放入该四棱锥形骨架内,使皮球的表面与8根铁丝都相切,则皮球的表面积为________.
正确答案
36π
解析
如图所示,原几何体为三棱锥D-ABC,
其中AB=BC=4,AC=4
故最长的棱的长度为DA=6.
又因为四棱锥形骨架的底面是一个正方形,一共有四条棱,又正方形的中心到四条棱的距离为3,所以皮球的表面与8根铁丝都相切时,球心为底面正方形的中心,所以球的半径是3 cm,所以球的表面积为36π.
知识点
扫码查看完整答案与解析