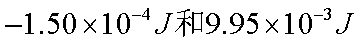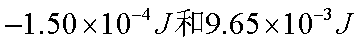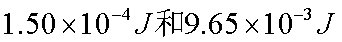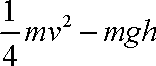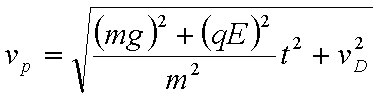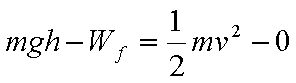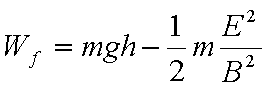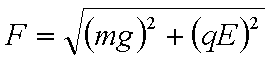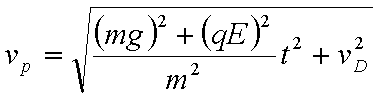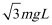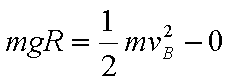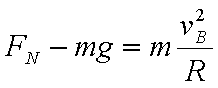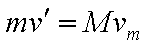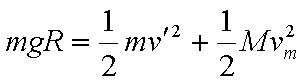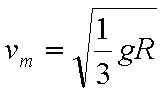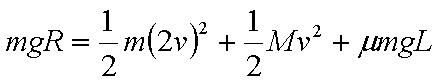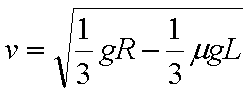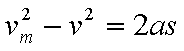- 功能关系
- 共276题
地球表面附近某区域存在大小为150N/C、方向竖直向下的电场。一质量为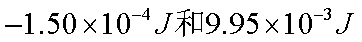
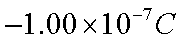
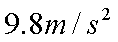
正确答案
解析
略
知识点
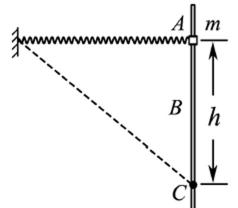
9.如图所示,轻质弹簧一端固定,另一端与一质量为m、套在粗糙竖直固定杆A处的圆环相连,弹簧水平且处于原长。圆环从A处由静止开始下滑,经过B处的速度最大,到达C处的速度为零,AC=h.圆环在C处获得一竖直向上的速度v,恰好能回到A. 弹簧始终在弹性限度内,重力加速度为g,则圆环
A.下滑过程中,加速度一直减小
B.下滑过程中,克服摩擦力做的功为
C.在C处,弹簧的弹性势能为
D.上滑经过B的速度大于下滑经过B的速度
正确答案
BD
解析
解析已在路上飞奔,马上就到!
知识点
18.如图,由某种粗细均匀的总电阻为3R的金属条制成的矩形线框abcd,固定在水平面内且处于方向竖直向下的匀强磁场B中。一接入电路电阻为R的导体棒PQ,在水平拉力作用下沿aB.dc以速度v匀速滑动,滑动过程PQ始终与ab垂直,且与线框接触良好,不计摩擦。在PQ从靠近ad处向bc滑动的过程中( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.(16分)一转动装置如图所示,四根轻杆OA、OC、AB和CB与两小球以及一小环通过铰链连接,轻杆长均为l,球和环的质量均为m,O端固定在竖直的轻质转轴上,套在转轴上的轻质弹簧连接在O与小环之间,原长为L,装置静止时,弹簧长为
(1)弹簧的劲度系数k;
(2)AB杆中弹力为零时,装置转动的角速度
(3)弹簧长度从

正确答案
(1)装置静止时,设





小环受到弹簧的弹力
小环受力平衡
小球受力平衡
解得
(2)设






小环受到弹簧的弹力
小环受力平衡 
对小球

解得
(3)弹簧长度为






小环受到弹簧的弹力
小环受力平衡
对小球
解得
整个过程弹簧弹性势能变化为零,则弹力做的功为零,由动能定理
解得
解析
解析已在路上飞奔,马上就到!
知识点
子弹射入静止于光滑水平地面上的木块,则( )
正确答案
解析
略
知识点
下列关系式中正确的是( )
正确答案
解析
略
知识点
22. 如图,绝缘粗糙的竖直平面MN左侧同时存在相互垂直的匀强电场和匀强磁场,电场方向水平向右,电场强度大小为E,磁场方向垂直纸面向外,磁感应强度大小为B。一质量为m、电荷量为q的带正电的小
(1)求小滑块运动到C点时的速度大小vc;
(2)求小滑块从A点运动到C点过程中克服摩擦力做的功Wf;
(3)若D点为小滑块在电场力、洛伦兹力及重力作用下运动过程中速度最大的位置,当小滑块运动到D点时撤去磁场,此后小滑块继续运动到水平地面上的P点。已知小滑块在D点时的速度大小为vD,从D点运动到P点的时间为t,求小滑块运动到P点时速度的大小vp。
正确答案
(1)E/B (2
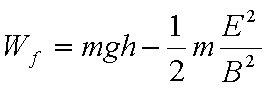
(1)由题意知,根据左手定则可判断,滑块在下滑的过程中受水平向左的洛伦兹力,当洛伦兹力等于电场力qE时滑块离开MN开始做曲线运动,即Bqv=qE
解得:v=E/B
(2)从A到C根据动能定理:
解得:
(3)设重力与电场力的合力为F,由图意知,在D点速度vD的方向与F地方向垂直,从D到P做类平抛运动,在F方向做匀加速运动a=F/m,t时间内在F方向的位移为
从D到P,根据动能定理: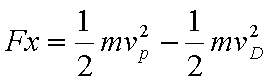
联立解得:
解析
解析已在路上飞奔,马上就到!
知识点
5.如图所示,固定的竖直光滑长杆上套有质量为m的小圆环,圆环与水平状态的轻质弹簧一端连接,弹簧的另一端连接在墙上,并且处于原长状态,现让圆环由静止开始下滑,已知弹簧原长为L,圆环下滑到最大距离时弹簧的长度变为2L(未超过弹性限度),则在圆环下滑到最大距离的过程中( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
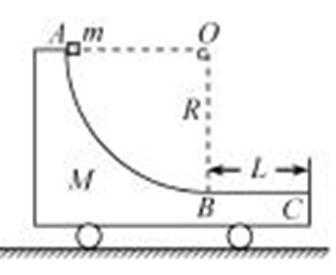
21.如图,质量为M的小车静止在光滑的水平面上,小车AB段是半径为R的四分之一圆弧光滑轨道,BC段是长为L的水平粗糙轨道,两段轨道相切于B点,一质量为m的滑块在小车上从A点静止开始沿轨道滑下,重力加速度为g。
(1)若固定小车,求滑块运动过程中对小车的最大压力;
(2)若不固定小车,滑块仍从A点由静止下滑,然后滑入BC轨道,最后从C点滑出小车,已知滑块质量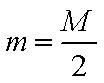
① 滑块运动过程中,小车
② 滑块从B到C运动过程中,小车的位移大小s。
正确答案
(1)3mg (2)①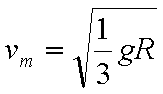
(1)由图知,滑块运动到B点时对小车的压力最大
从A到B,根据动能定理:
在B点:
联立解得

(2)①若不固定小车, 滑块到达B点时,小车的速度最大
根据动量守恒可得:
从A到B,根据能量守恒:
联立解得:
②设滑块到C处时小车的速度为v,则滑块的速度为2v,根据能量守恒:
解得:
小车的加速度:
根据
解得:s=L/3
解析
解析已在路上飞奔,马上就到!
知识点
23.如图甲所示,物块与质量为m的小球通过不可伸长的轻质细绳跨过两等高定滑轮连接。物块置于左侧滑轮正下方的表面水平的压力传感装置上,小球与右侧滑轮的距离为

求:
(1)物块的质量;
(2)从释放到运动至最低位置的过程中,小球克服空气阻力所做的功。
正确答案
(1)3m;
(2)0.1mgl;
解析:对小球摆到最低点的过程,根据动能定理可知:
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析