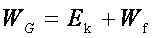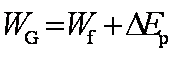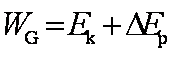- 功能关系
- 共276题
如图，竖直放置的轻弹簧，下端固定，上端与质量为
正确答案
0, 2
解析
略
知识点
如图，在光滑绝缘水平面上有两个带电量分别为＋q、－2q的小球，由静止开始释放两球，
则两球相互靠近的过程中，对两球组成的系统（ ）
正确答案
解析
略
知识点
如图，质量为m的木块在水平向右的力F作用下在质量为M的木板上滑行，木板长度为L，保持静止，木块与木板、木板与地面间的动摩擦因数均为μ，说法正确的是
正确答案
解析
略
知识点
如图甲所示，两固定的竖直光滑金属导轨足够长且电阻不计，两质量、长度均相同的导体棒c、d，置于边界水平的匀强磁场上方同一高度h处，磁场宽为3h，方向与导轨平面垂直，先由静止释放c，c刚进入磁场即匀速运动，此时再由静止释放d，两导体棒与导轨始终保持良好接触，用ac表示c的加速度，Ekd表示d的动能，xc、xd分别表示c、d相对释放点的位移，图乙中正确的是：（ ）
A
B
C
D
正确答案
解析
略
知识点
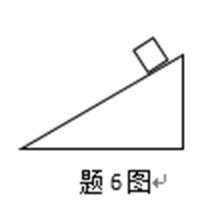
如图所示，一物块由静止开始从粗糙斜面上的一点加速下滑到另一点，在此过程中重力做功为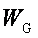
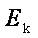
A
B
C
D
正确答案
解析
略
知识点
一个倾角为45°的光滑斜面处于水平的匀强电场之中，如图所示(图中未标出电场方向)，带负电的质量为m的物体沿此斜面匀速下滑，则下列说法中正确的是
A电场的方向水平向左
B物体下滑过程中机械能增加
C物体下滑过程中电势能增加
D电场力的大小为
正确答案
解析
物体匀速下滑，受重力mg、支持力N、电场力F平衡，其中电场力的方向水平向右，由于物体带负电，故电场方向水平向左，A对；物体匀速下滑，动能不变，重力势能减少，机械能减少，机械能转化为电势能，B错；电场力做负功，电势能增加，C对；电场力的大小为F=mgtan45°=mg，D错。
知识点
质量为m的跳水运动员从距水面H高处跳下，落入水中后受到水的阻力而做减速运动，不计空气阻力，设水对他的阻力大小恒为F，运动员从离开跳台到落入水中减速下降h高度的过程中，他的重力势能减少了 ，他的机械能减少了 。
正确答案
mg(H+h) ，Fh
解析
略
知识点
如图（a）为用DIS做“测定电动机效率”的实验装置，图（b）是用位移传感器测定重物匀速上升时的位移——时间图线，同时电流传感器和电压传感器的读数基本不变，约为0.14A和3.3V，已知重物质量
正确答案
0.25，54.1%
解析
略
知识点
如图10甲所示，表面绝缘、倾角
（1）求线框受到的拉力F的大小；
（2）求匀强磁场的磁感应强度B的大小；
（3）已知线框向下运动通过磁场区域过程中的速度v随位移x的变化规律满足v＝v0-
正确答案
见解析。
解析
（1）由v-t图象可知，在0～0.4s时间内线框做匀加速直线运动，进入磁场时的速度为v1=2.0m/s，所以在此过程中的加速度 a=
由牛顿第二定律
解得 F=1.5 N
（2）由v-t图象可知，线框进入磁场区域后以速度v1做匀速直线运动，
产生的感应电动势 E=BLv1
通过线框的电流 I=
线框所受安培力 F安=BIL=
对于线框匀速运动的过程，由力的平衡条件，有
解得 B=0.50T
（3）由v-t图象可知，线框进入磁场区域后做匀速直线运动，并以速度v1匀速穿出磁场，说明线框的宽度等于磁场的宽度 D=0.40m
线框ab边离开磁场后做匀减速直线运动，到达档板时的位移为s-D=0.15m
设线框与挡板碰撞前的速度为v2
由动能定理，有 
解得 v2=
线框碰档板后速度大小仍为v2，线框下滑过程中，由于重力沿斜面方向的分力与滑动摩擦力大小相等，即mgsinθ=μmgcosθ=0.50N，因此线框与挡板碰撞后向下做匀速运动，ab边刚进入磁场时的速度为v2=1.0 m/s；进入磁场后因为又受到安培力作用而减速，做加速度逐渐变小的减速运动，设线框全部离开磁场区域时的速度为v3
由v＝v0-
因v3<0，说明线框在离开磁场前速度已经减为零，这时安培力消失，线框受力平衡，所以线框将静止在磁场中某位置。
线框向上运动通过磁场区域产生的焦耳热Q1=I2Rt=
线框向下运动进入磁场的过程中产生的焦耳热Q2=
所以Q= Q1+ Q2=0.45 J
知识点
“蹦极”运动是勇敢者的运动。蹦极运动员将弹性长绳（质量忽略不计）的一端系在双脚上，另一端固定在高处的跳台上，运动员无初速地从跳台上落下。若不计空气阻力，对于运动员的第一次下落过程，以下说法中正确的是 （ ）
正确答案
解析
略
知识点
扫码查看完整答案与解析