- 圆锥曲线的定点、定值问题
- 共61题
20. 已知左焦点为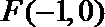

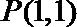
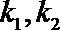
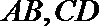
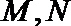
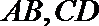
(1)求椭圆的标准方程;
(2)若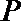
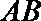
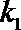
(3)若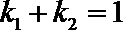
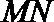
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知椭圆
(1)求椭圆E的方程;
(2)若M,N是直线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
23.给定椭圆






(1)求椭圆
(2)点






①当


②求证:
正确答案
(1)
所以,椭圆方程:
准圆方程:
(2)①易知
设直线为
联立
因为椭圆与直线有且只有一个交点,
所以
所以
②<ⅰ>当

设直线
由
同理,联立

由(*)(**)可知,


因此
<ⅱ>当

所以
解析
解析已在路上飞奔,马上就到!
知识点
20.已知椭圆




(1)(ⅰ)若圆

(ⅱ)若椭圆上存在点


(2)设直线




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.如图,已知抛物线














(1)求圆

(2)若


(3)过直线




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析






















