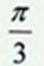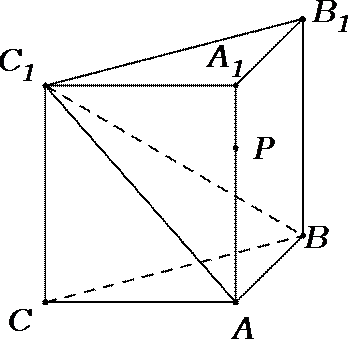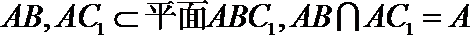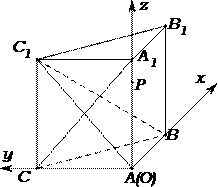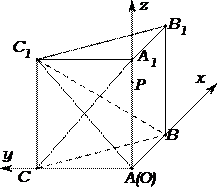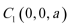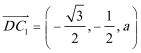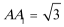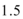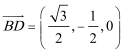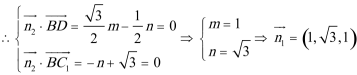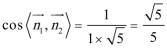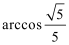- 线面角和二面角的求法
- 共279题
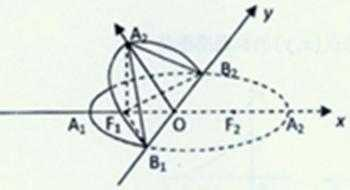
15.如图,椭圆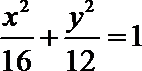
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.如图,侧棱垂直底面的三棱柱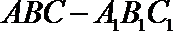
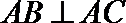
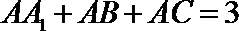
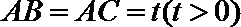
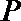
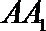
(Ⅰ)当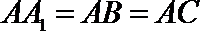
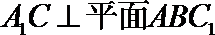
(Ⅱ)试求三棱锥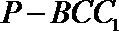
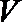
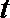
(Ⅲ)若二面角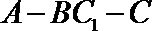
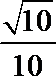
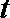
正确答案
(Ⅰ)证法一:∵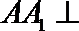
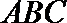
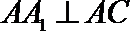
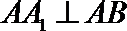
又∵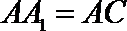
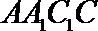
∴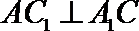
∵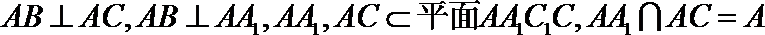
∴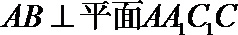
又∵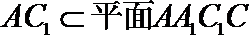
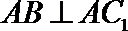
∵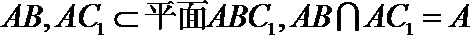
∴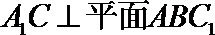
证法二:
∵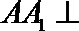
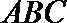
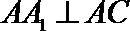
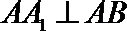
又∵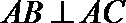
∴分别以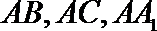
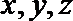
则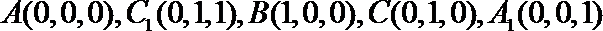
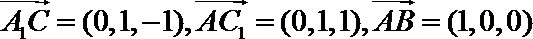
∴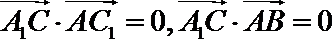
∴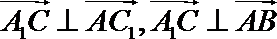
又∵
∴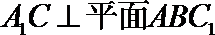
证法三:
∵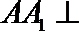
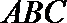
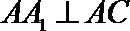
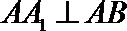
又∵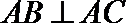
∴分别以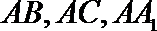
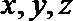
则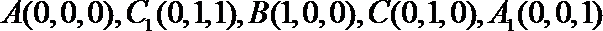
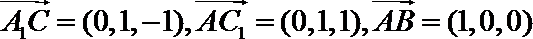
设平面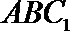
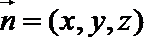
则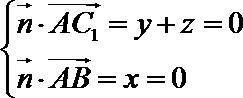
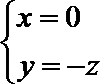
令
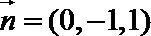
∵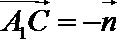
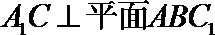
(Ⅱ)∵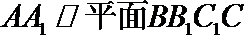
∴点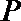
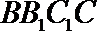
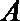
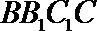
∴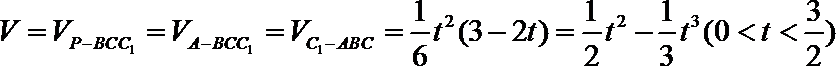
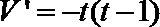
令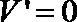
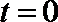
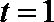
得
∴当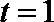
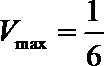
(Ⅲ)
分别以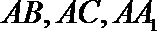
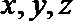
则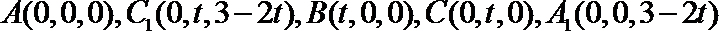
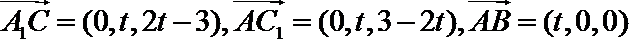
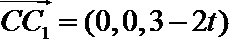
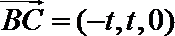
设平面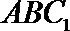
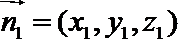
则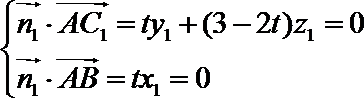
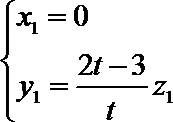
令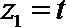
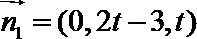
设平面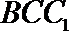
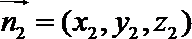
则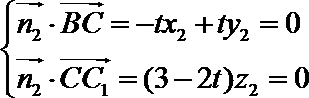
由于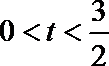
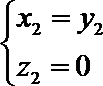
令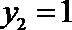
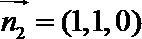
设二面角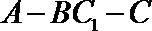
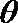
则有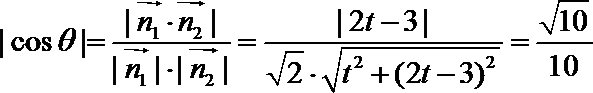
化简得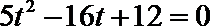
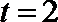
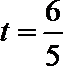
所以当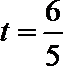
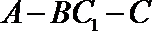
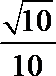
解析
解析已在路上飞奔,马上就到!
知识点
18.如图,在平行四边形









(1)求证:
(2)求证:BF∥平面
(3)直线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.如图,正方形ABCD、ABEF的边长都是1,而且平面ABCD、ABEF互相垂直,点M在AC上移动,点N在BF上移动,若CM=BN=a(0<a<
(1)求MN的长;
(2)a为何值时,MN的长最小;
(3)当MN的长最小时,求面MNA与面MNB所成二面角α的大小.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知二面角







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.如图示,已知平行四边形ABCD和矩形ACEF所在平面互相垂直,AB=1,AD=2,
(1)求证:
(2)设二面角A—FD—B的大小为

(3)设点P为一动点,若点P从M出发,沿棱按照
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.如图:PA⊥平面ABCD,ABCD是矩形,PA=AB=1,PD与平面ABCD所成角是30°,点F是PB的中点,点E在边BC上移动。
(Ⅰ)点E为BC的中点时,试判断EF与平面PAC的位置关系,并说明理由;

(Ⅲ)当BE等于何值时,二面角P-DE-A的大小为45°。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
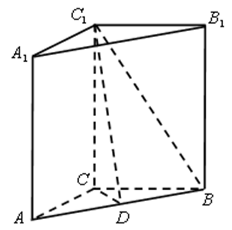
19.如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,2AC=AA1=BC=2.

(1)若D为AA1中点,求证:平面B1CD⊥平面B1C1D;
(2)当AD的长等于多少时?二面角B1-DC-C1的大小为60°.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.在直三棱柱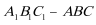
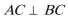
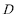
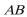
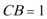
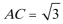
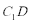
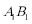
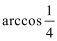
(1)求三棱柱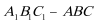
(2)求二面角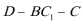
正确答案
(1)如图建立空间直角坐标系
设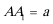
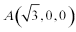
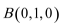
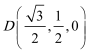
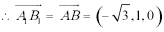
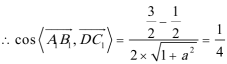
解得
可得:三棱柱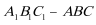
(2)显然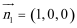
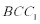
设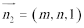
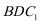
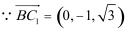
所以二面角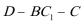
解析
解析已在路上飞奔,马上就到!
知识点
18.四棱锥






(1)求证:
(2)求二面角
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析