- 线面角和二面角的求法
- 共279题
18.如图,在三棱柱




(Ⅰ)求证:
(Ⅱ)设





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
23. 已知四棱锥







(1)求异面直线

(2)若

(3)是否存在


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.如图,斜三棱柱




(Ⅰ)证明:


(Ⅱ)在平面


正确答案
解:(Ⅰ)面





所以

取






















(Ⅱ)在






在













且


解析
解析已在路上飞奔,马上就到!
知识点
19.如图,在三棱锥A—BCD中,∠ABC=∠BCD=∠CDA=90°,AC=
(I)求证:CE⊥ BD:
(II)设点G在棱AC上,且CG=2GA,试求二面角C一EG—D的余弦值。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.如图,在四棱锥









(1)求证:平面

(2)求平面

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.在正方形








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.如图(a)所示,在边长为2的正方形ABB1A1中,C,C1分别是AB,A1B1的中点,现将正方形ABB1A1沿CC1折叠,使得平面ACC1A1

(1)当E是棱CC1中点时,求证:
(2)在棱CC1上是否存在点E,使得二面角A—EB1—B的大

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.在多面体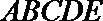
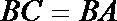
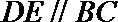
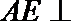
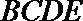
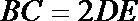
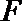
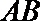
(I)求证: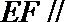
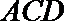
(II)若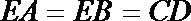
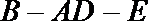
正确答案
证明:(Ⅰ)取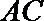
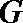
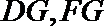
因为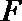
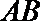
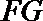
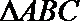
则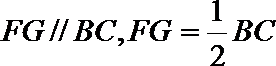
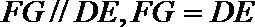
则四边形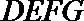
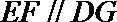
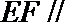
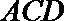
(Ⅱ)过点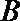
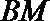
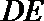
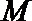
因为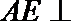
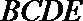
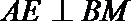
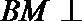
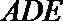
过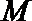
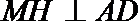

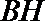
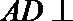
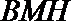
所以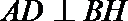
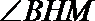
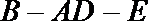
设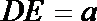
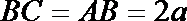
在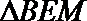
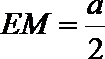
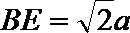
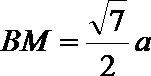
又因为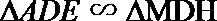
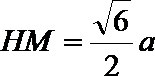
解析
解析已在路上飞奔,马上就到!
知识点
10.如图,正方体ABCD-A1B1C1D1 的棱长为2,棱A1B1的中点为P,则点C到平面D1DP的距离为_______.
正确答案
解析
如图,以D为坐标原点,建立如图所示的空间直角坐标系Dxyz.
由题设知正方体的棱长为2,则D(0,0,0),A(2,0,0),B1(2,2,2),A1(2,0,2),D1(0,0,2),C(0,2,0),P(2,1,2),设平面D1DP的法向量n=(x,y,z),

则
即
∴n的一个取值为(-1,2,0).又
∴点C到平面D1DP的距离
知识点
6.在棱长为a的正方体ABCD-A1B1C1D1中,M是AA1的中点,则点C1到平面MBD的距离是( ).
正确答案
解析
以点D为坐标原点,DA,DC,DD1所在的直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系,
则D(0,0,0),B(a,a,0),M(a,0,
∴




设n=(x,y,z)为平面MBD的一个法向量,
则
即


∴点C1到平面MBD的距离d=
知识点
扫码查看完整答案与解析