- 线面角和二面角的求法
- 共279题
19.(本小题满分12分)




(I)证明:
(II)求二面角
正确答案
知识点
18.(本小题满分12分)
如图,在四棱锥P-ABCD中,AD∥BC,


(I)在平面PAB内找一点M,使得直线CM∥平面PBE,并说明理由;
(II)若二面角P-CD-A的大小为45°,求直线PA与平面PCE所成角的正弦值.
正确答案
知识点
(本小题满分12分)




(I)证明:
(II)求二面角
正确答案
(I)由已知得




因此




由



于是

故
又

所以
(II)如图,以

























知识点
18.如图,在三棱柱













(Ⅰ)证明,

(Ⅱ)求二面角
正确答案
(Ⅰ)证明:因为



因为




所以
因为




又因为



所以

(Ⅱ)解法一,连接



过



由(Ⅰ)知,

所以平面

所以


所以


故


设




又




在



从而

所以
因为
所以
故二面角

解法二,设












则

因为



故
所以


设平面

则

从而


所以

设平面

则

从而


所以

设二面角


则

故二面角

解析
设












则

因为



故
所以


设平面

则

从而


所以

设平面

则

从而


所以

设二面角


则

故二面角

考查方向
本题考查了立体几何的基本问题,分类讨论讨论点大体可以分成以下几类:
1、线面垂直问题;
2、二面角问题。
解题思路
1、选取合适的单位长度,根据图像的框架结构建立合适的直角坐标系。
2、确定问题所需的点的坐标。
易错点
本题如果利用纯几何法,第一问相较容易,但是第二问找二面角难度较大,而且本题建立直角坐标系的垂直的三线是现成的,所以本题建议用空间向量法解决以提高正确率。
知识点
(本小题满分14分)














(Ⅰ)求证:
(Ⅱ)当点


弦值;
(Ⅲ)是否存在点


正确答案
考查方向
易错点
1、第二问判断二面角是锐角还是钝角时易出错。
知识点
16.多面体ABCDEF(如图甲)的俯视图如图乙,己知面ADE为正三角形.
(1)求多面体ABCDEF的体积;
(2)求二面角A-BF-C的余弦值.
正确答案
(1)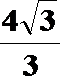
(2)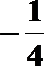
解析
试题分析:本题属于立体几何中的基本问题,题目的难度是逐渐由易到难.
(1)分别取AB、CD的中点M、N,连接EM、EN、MN,多面体体积转化为棱柱AED-MFN的体积V1与四棱锥F-MBCN的体积V2之和。
由三视图可知,AD=2,AM=DN=1,面ADE为正三角形且垂直于底面ABCD,知F点到底面的距离为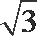
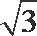
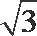
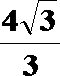
(2) 取MN的中点O,BC的中点P,以OM为x轴,OP为y轴,OF为z轴建立坐标系,
易知A(1,-1,0),B(1,1,0),F(0,0, 
设面ABF的法向量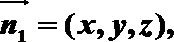
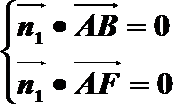
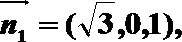
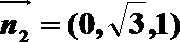

考查方向
本题考查了立体几何中的体积和二面角的问题.属于高考中的高频考点。
解题思路
本题考查立体几何中的体积和二面角的问题,解题步骤如下:
(1)做辅助线,拆分多面体。
(2)建立空间直角坐标系。
(3)利用夹角的余弦公式求解。
易错点
(1)第一问中的多面体的拆分。
(2)第二问中二面角的求解时要建立适当的空间直角坐标系。
知识点
19.已知四棱柱






(1)求证:直线

(2)已知




正确答案
(1)略
(2)
解析
(1)证明:关键步骤:

(2)由已知可得四棱柱













考查方向
本题主要考查了直线与平面垂直的判定和性质,以及利用空间坐标系求二面角的方法等知识。
解题思路
(1)由线线垂直推出线面垂直。
(2)建立空间坐标系,求法向量,最后求出二面角。
易错点
(1)第一问推理不够严密。
(2)法向量求错,从而导致结果错误。
知识点
18. 如图,在四棱锥S—ABCD中,底面ABCD是直角梯形,侧棱SA丄底面ABCD,AB垂直于AD 和 BC,SA=AB = BC=2,AD = 1.M 是棱 SB 的中点.
(1)求证:AM/
(2)求平面SCD与平面SAB所成的二
(3)设点N是直线CD上的动点,MN与平面SAB所成的角为0,求sin
正确答案
(2)
解析
试题分析:(Ⅰ)通过建立空间直角坐标系,利用平面SCD的法向量
(Ⅰ)以点A为原点建立如图所示的空间直角坐标系,则
A(0,0,0),B(0,2,0),D(1,0,0,),S(0,0,2),M(0,1,1).
则


设平面SCD的法向量是
则

于是
∵

(Ⅱ)易知平面SAB的法向量为





(Ⅲ)设N(x,2x﹣2,0),则
∴



当


考查方向
用空间向量求平面间的夹角;直线与平面平行的判定;直线与平面所成的角;二面角的平面角及求法.菁优网版权所有
解题思路
建立空间直角坐标系利用平面SCD的法向量
易错点
1、利用定义求通项公式
2、第二问中错位相减法计算的准确性;
知识点
17.如图,在四棱锥










(Ⅰ)求证:

(Ⅱ)若



(Ⅲ)如果直线




正确答案
(Ⅰ)证明略;
(Ⅱ)证明略;
(Ⅲ)
解析
试题分析:本题属于立体几何的基本问题,题目的难度是逐渐由易到难,(1)直接按照步骤来求,(2)要注意判定定理的条件要全
(Ⅰ)证明:在平行四边形


所以
由


所以
因为侧面


所以

又因为

所以
又因为




所以

(Ⅱ)证明:因为



所以
又因为



所以

同理,得

又因为




所以平面

又因为

所以

(Ⅲ)解:因为



分别为


则
所以


设

所以

易得平面

设平面

由

令

因为直线


所以

所以 
解得

考查方向
本题主要考查了空间中直线与平面的位置关系的转化、空间向量在立体几何中的运用;空间中线面位置关系的证明值域有以下几类:
1.线线间的平行或垂直,
2.面面间的平行或垂直,
3.线面间的平行或垂直;
空间向量在立体几何中的运用,主要分以下几类:
1.利用空间向量求异面直线的角,
2.利用空间向量求直线与平面所成的角,
3.利用空间向量求二面角,
4.利用空间向量求点到平面的距离.
解题思路
本题考查立体几何问题,解题步骤如下:
1.利用线面垂直的判定定理进行证明;
2.利用三角形的中位线得到线线平行,利用线面平行的判定定理得到线面平行;
3.利用面面平行的判定定理进行证明;
4.建立空间直角坐标系,利用三点共线设点,求出平面的法向量;5.利用两角相等求得比值。
易错点
1、第一、二问中,利用判定定理证明时,条件不全;
2、第三问中写点的坐标出现错误。
知识点
(12分)(2015•上海)如图,在长方体ABCD﹣A1B1C1D1中,AA1=1,AB=AD=2,E、F分别是AB、BC的中点,证明A1、C1、F、E四点共面,并求直线CD1与平面A1C1FE所成的角的大小.
正确答案
连接AC,因为E,F分别是AB,BC的中点,所以EF是△ABC的中位线,所以EF∥AC.由长方体的性质知AC∥A1C1,
所以EF∥A1C1,
所以A1、C1、F、E四点共面.
以D为坐标原点,DA、DC、DD1分别为xyz轴,建立空间直角坐标系,易求得

设平面A1C1EF的法向量为
则


z=1,得x=1,y=1,所以
所以

所以直线CD1与平面A1C1FE所成的角的大小arcsin
知识点
扫码查看完整答案与解析