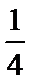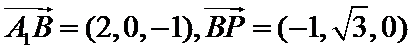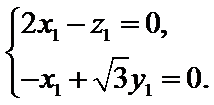- 线面角和二面角的求法
- 共279题
如图,在四棱锥









22.求证:平面

23.求点

正确答案
见解析
解析
试题分析:本题属于立体几何中的基本问题,题目的难度是逐渐由易到难,根据题设先证线面垂直再去证面面垂直;证明:取






















考查方向
解题思路
本题考查了面面垂直的证明和点到面的距离的求,解题步骤如下:根据题设先证线面垂直再去证面面垂直。
易错点
对面面垂直的证明的表述不严谨和运算出错
正确答案
解析
试题分析:本题属于立体几何中的基本问题,题目的难度是逐渐由易到难,由等体积法求出点到面的距离。由⑴知,
∴








∴点


考查方向
解题思路
本题考查了面面垂直的证明和点到面的距离的求,解题步骤如下:由等体积法求出点到面的距离。
易错点
对面面垂直的证明的表述不严谨和运算出错
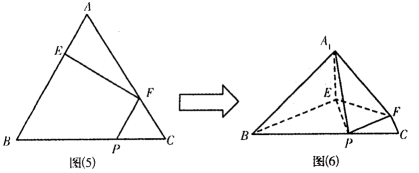
在正三角形ABC中,E、F、P分别是AB、AC、BC边上的点,满足AE :EB=CF :FA=CP :PB=1 :2,如图(5).将△AEF沿EF折起到△A1EF的位置,使二面角A1一EF-B成直二面角,连结A1B、A1P,如图(6).
21.求证:A1E⊥平面BEP;
22.求二面角B—A1P—E的余弦值.
正确答案
(1)A1E⊥平面BEP;
解析
解:不妨设正三角形ABC 的边长为 3 .
(1)在图5中,取BE的中点D,连结DF.
∵AE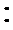
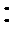
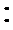
又AE=DE=1,∴EF⊥AD
在图6中,A1E⊥EF,BE⊥EF,∴∠A1EB为二面角A1-EF-B的平面角.
由题设条件知此二面角为直二面角,∴A1E⊥BE
又BE∩EF=E,∴A1E⊥平面BEF,即A1E⊥平面BEP
考查方向
解题思路
(1)不妨设正三角形ABC 的边长为 3,取BE的中点D,连接DF,从而证明到EF⊥AD,再利用二面角A1一EF-B成直二面角推出A1E⊥BE,从而得证。
(2)由(1)构建空间直角坐标系并写出相关点的坐标,通过计算平面法向量的方法来计算二面角的余弦值。
易错点
平面翻折到空间中的不变量与改变量易出错及空间点坐标的确定。
正确答案
(2) 二面角B-A1P-E余弦值是
解析
解:
(2)建立分别以EB、EF、EA1为x轴、y轴、z轴的空间直角坐标系,则E(0,0,0),A1(0,0,1),
B(2,0,0),F(0, 
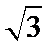
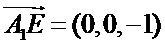

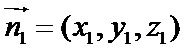
由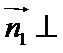
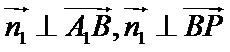
令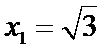

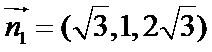
设平面A1PE向量为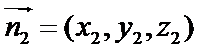
由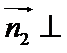
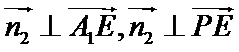


考查方向
解题思路
(1)不妨设正三角形ABC 的边长为 3,取BE的中点D,连接DF,从而证明到EF⊥AD,再利用二面角A1一EF-B成直二面角推出A1E⊥BE,从而得证。
(2)由(1)构建空间直角坐标系并写出相关点的坐标,通过计算平面法向量的方法来计算二面角的余弦值。
易错点
平面翻折到空间中的不变量与改变量易出错及空间点坐标的确定。



18.若平面


19.求平面
正确答案
见解析
解析
考查方向
解题思路
该题解题关键在于找到所求内容的突破点
确定线面平行判定的方式:线//面→线//线
由已知AD//BC,得到线//面
易错点
本题容易在辅助线建立过程出错,空间直角坐标系建立及其坐标表示出错,二面角的判断出错
正确答案
见解析
解析
考查方向
解题思路
该题解题关键在于找到所求内容的突破点
根据线//面→线//线
根据已知条件建立坐标系,并标记所需点的坐标
计算相应面的法向量,并求向量的夹角
判断两面角的大小确定二面角
易错点
本题容易在辅助线建立过程出错,空间直角坐标系建立及其坐标表示出错,二面角的判断出错
15.如图,正四面体




绕


正确答案
解析
过A作






考查方向
解题思路
结合正四面体的性质,利用三余弦公式可求解,
易错点
找不到解决问题的几何模型易了出错。
知识点
8.如图,已知△ABC,D是AB的 中点,沿直线CD将△ACD折成△A′CD,所成二面角A′-CD-B的平面角为α,则( )
正确答案
解析
试题分析:分AC=BC和AC≠BC两种情况,作出二面角的平面角进行判断。
当AC=BC时,∠A′DB为二面角A′-CD-B的平面角,∠A′DB=α;
当AC≠BC时,∠A′DB>α,故选B.
考查方向
解题思路
作出二面角的平面角,然后进行判断即可。
易错点
注意角的关系中等号成立的条件。
知识点
如图,








18.求证:
19.当三棱锥






正确答案
见证明.
解析
试题分析:本题属于立体几何的综合应用问题,属于中档题,只要掌握相关立体几何的知识,即可解决本题,解析如下:证明:因为






考查方向
解题思路
直接利用线面垂直的判定定理进行证明;
易错点
相关知识不熟容易处错。
正确答案
不存在.
解析
试题分析:本题属于立体几何的综合应用问题,属于中档题,只要掌握相关立体几何的知识,即可解决本题,解析如下:不存在.
证明如下:
当面




所以

(方法一)连结
因为

所以









设




因为

(方法二)(前面同解法一)在直角三角形






(方法三)已证得

则









考查方向
解题思路
本问题方法较多,可以直接进行证明,也可以利用向量进行证明,详见解析.
易错点
相关知识不熟容易处错。
如图,已知四棱锥P-ABCD,底面ABCD为蓌形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC 的中点.
21.求证:AE⊥PD;
22.若直线PB与平面PAD所成角的正弦值为
正确答案
见解析
解析
证明:由四边形



因为E为BC的中点,所以AE⊥BC.又BC∥AD,因此AE⊥AD.
因为PA

而PA

所以 AE⊥平面PAD,又PD
考查方向
解题思路
第1问通过线面垂直证明线线垂直,第2问先找到二面角的平面角,然后在根据相关线段长求二面角的余弦值。
易错点
计算错误;空间直角坐标系建立错误
正确答案
见解析
解析
由21知AE,AD,AP两两垂直,以








所以




由





解得



设平面AEF的一法向量为m=(x1,y1,z1),则







所以

因为二面角E-AF-C为锐角,所以所求二面角的余弦值为
考查方向
解题思路
第1问通过线面垂直证明线线垂直,第2问先找到二面角的平面角,然后在根据相关线段长求二面角的余弦值。
易错点
计算错误;空间直角坐标系建立错误
如图,三棱柱







21.求证:

22.求二面角
正确答案
(1)略;
解析
(Ⅰ)依题意,侧面




又平面




所以

考查方向
解题思路
先证明


易错点
不会转化平面

正确答案
(2)
解析
(Ⅱ)由(Ⅰ)知




又



过




所以

在

所以
所以


考查方向
解题思路
先证明

易错点
找不到二面角的平面角无法做出答案。
如图(1)所示,在直角梯形ABCD中,AD∥BC,∠BAD=,AB=BC=1,AD=2,E是AD的中点,O是AC与BE的交点.将△ABE沿BE折起到△A1BE的位置,如图(2)所示.
22.证明:CD⊥平面A1OC;
23.若平面A1BE⊥平面BCDE,求平面A1BC与平面A1CD所成锐二面角的余弦值.
正确答案
见解析
解析
证明:在图(1)中,因为
考查方向
解题思路
第1问利用面面垂直证明线面垂直,第2问先找到二面角的平面角,再利用解直角三角形性质求解。
易错点
找不到二面角,辅助线作不出来
正确答案
见解析
解析
由已知
所以∠A1OC为二面角A1BE C的平面角,所以∠A1OC=.如图,以O为原点,OB,OC,OA1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,
因为A1B=A1E=BC=ED=1,BC∥ED,所以B(,0,0)E(-,0,0),A1(0,0,),C(
==(-,0,0).设平面A1BC的法向量n1=(x1,y1,z1),平面A1CD的法向量n2=(x2,y2,z2),平面A1BC与平面A1CD的夹角为θ,
则得取n1=(1,1,1);
得取n2=(0,1,1),从而cos θ=|cos〈n1,n2〉|==,即平面A1BC与平面A1CD所成锐二面角的余弦值为.
考查方向
解题思路
第1问利用面面垂直证明线面垂直,第2问先找到二面角的平面角,再利用解直角三角形性质求解。
易错点
找不到二面角,辅助线作不出来
如图,三棱柱




侧面



18.证明:直线

19.求二面角
正确答案
【见解析】
解析
解:∵


∴ 
又 

又 


取



以


∴
(Ⅰ)设平面






∴ 




考查方向
解题思路
先计算必要棱长,证出


以



易错点
在证明线面平行时,没有严格按照定理的三个条件去证,重点是线线平行。易在过程的严密性上扣分。
正确答案
解析
解:∵


∴ 
又 

又 


取



以


∴
(Ⅱ)设平面





又由(Ⅰ)知平面



∵ 二面角

∴ 二面角

考查方向
解题思路
直接按步计算,先求法向量,再求法向量夹角,最后确定二面角余弦值与法向量夹角的余弦值之间的关系
易错点
建立合理的坐标系,正确求点坐标
扫码查看完整答案与解析