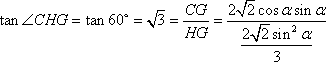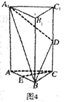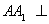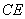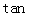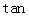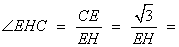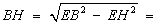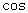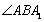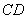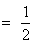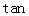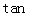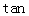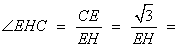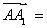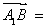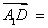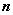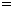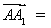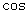- 线面角和二面角的求法
- 共279题
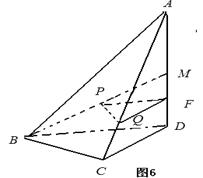
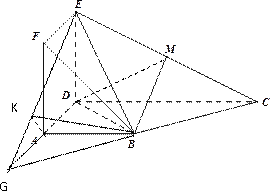
如图,在四面体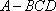
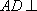
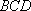
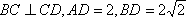
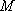
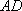
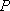
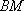
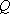
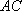
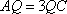
(1)证明: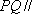
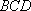
(2)若二面角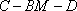
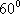
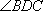
正确答案
见解析。
解析
(1)方法一:如图6,取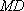
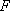
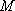
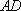
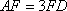
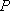
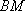
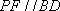
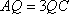
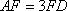
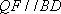
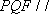
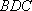
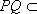
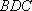
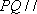
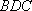
方法二:
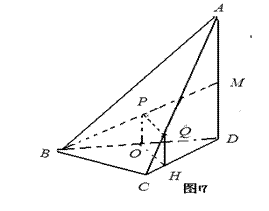
如图7所示,取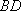

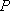
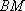
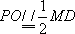
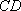
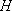
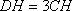
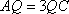
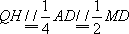
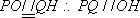
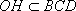
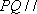
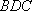
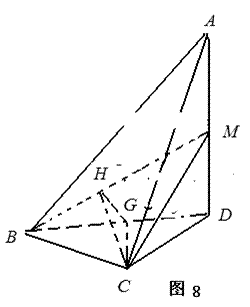
(2)如图8所示,由已知得到面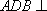
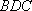
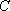
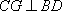
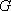

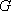
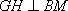
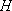
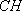
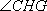
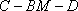
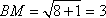
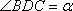
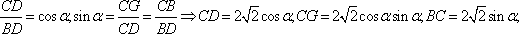
在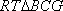
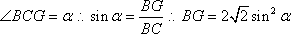
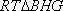
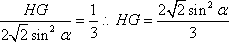
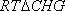
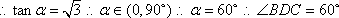
知识点
如图6所示,平面







(1)求证

(2)求平面

(3)求直线

正确答案
见解析。
解析
(法一)(1)
取






















(2)过点


于

















又







即平面


(3)
过点











又




又












即直线


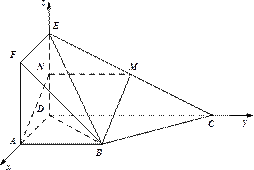
(法二)(1)





又


平面



以






根据题意我们可得以下点的坐标:












又


(2)设平面











设平面


则
因此,平面


(3)根据(2)知平面



设直线



因此,直线


知识点
如图












(1)求三棱锥
(2)求平面

正确答案
见解析。
解析
(1)∵平面






∴



又∵


∴

∴

∴三棱锥

(2)方法一:
∵



又∵





∴
∵
∴
∴
由已知可知
∵

∵


所以平面


方法二:
过E作直线

如图建立空间直角坐标系,则




则

令



同理可得平面PCD的一个法向量为
设向量


∴平面


知识点
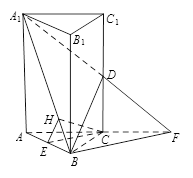
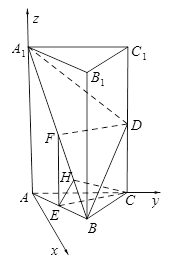
如图4,在三棱柱ABC-A1B1C1中,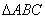
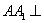
(1)求证:CE//平面A1BD;
(2)若H为A1B上的动点,当CH为平面A1AB所成最大角的正切值为
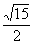
正确答案
见解析。
解析
解法一:
(1)证明:延长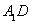
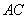
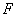
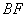
∵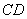
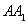
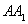
∴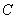
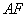
∵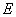
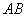
∴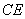
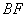
∵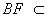
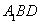
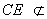
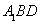
∴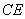
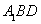
(2)解:∵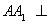
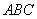
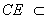
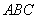
∴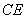
∵△
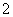
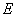
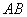
∴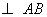
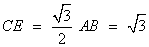
∵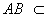
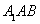
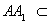
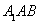
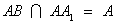
∴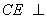
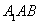
∴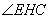
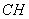
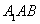
∵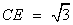
在Rt△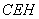
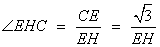
∴当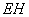
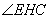
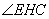
∴当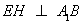
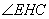
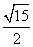
∴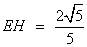
∵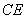
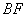
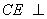
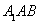
∴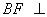
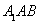
∵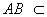
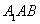
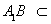
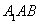
∴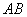
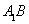
∴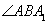
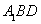
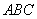
在Rt△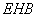
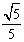
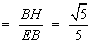
∴平面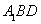
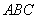
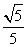
解法二:
(1)证明:取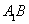
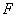
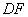
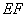
∵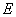
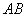
∴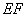
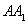
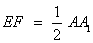
∵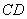
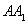
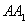
∴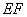
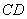
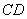
∴四边形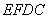
∴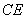
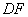
∵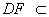
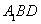
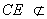
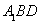
∴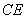
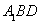
(2)解:∵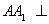

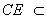
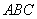
∴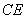
∵△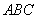
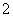
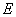
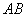
∴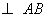
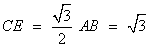
∵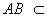
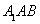
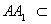
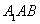
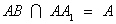
∴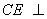
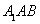
∴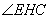
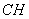
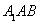
∵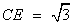
在Rt△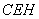
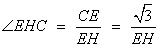
∴当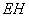
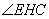
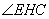
∴当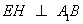
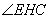
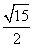
∴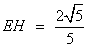
在Rt△
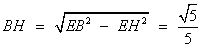
∵Rt△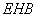
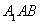
∴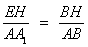
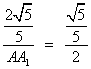
∴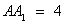
以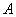
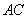
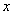
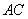
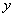
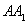
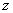
建立空间直角坐标系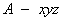
则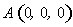
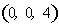
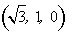
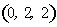
∴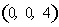
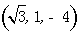
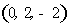
设平面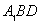
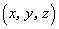
由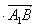
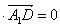
得
令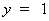
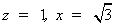
∴平面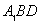
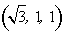
∵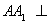
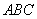
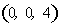
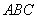
∴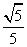
∴平面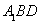
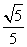
知识点
如图,正方形
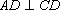
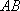
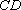

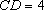

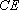
(1)求证: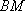
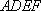
(2)求证:平面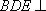
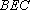
(3)求平面

正确答案
见解析。
解析
(1)证明:取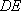
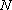
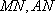
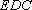
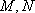
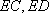
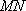
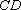
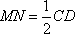
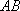
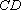
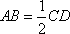
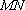
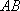
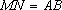
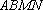
所以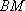
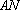
又因为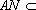
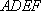
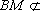
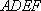
所以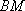
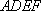
(2)证明:在正方形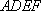
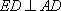
平面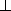
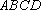
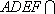
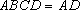
所以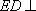
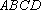
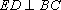
在直角梯形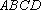
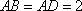
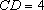
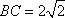
在△
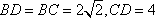
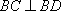
所以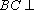
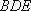
又因为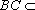
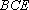
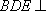
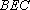
(3)(方法一)延长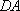
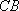
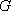
内过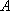
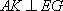
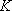
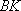
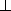
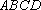
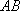
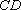
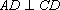

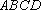
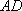
得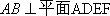
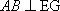
又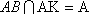
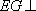
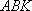
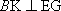
于是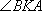
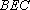
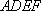
平面角。
由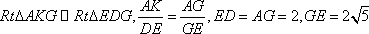
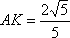
又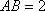
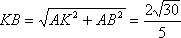
在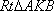
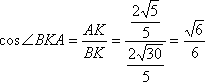
所以平面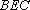
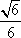
(方法二)
由(2)知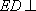
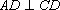
以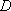
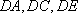
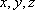
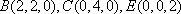
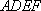
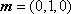
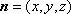
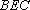
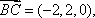
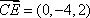
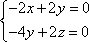
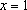
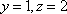
所以
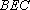
设平面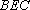

则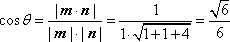
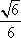
知识点
扫码查看完整答案与解析