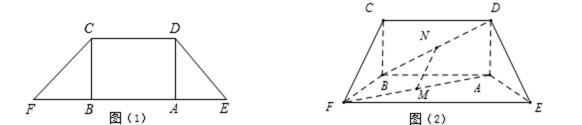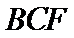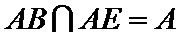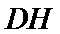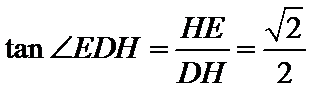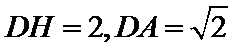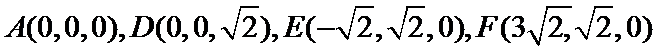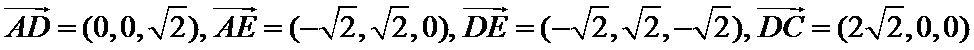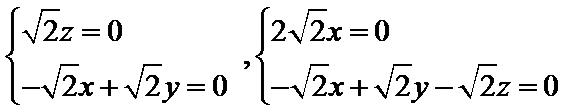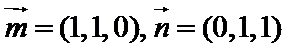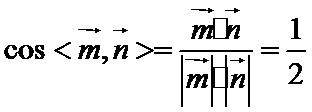- 线面角和二面角的求法
- 共279题
12. 已知在正方体




正确答案
解析
以








设直线



考查方向
解题思路
1.建立空间直角坐标系,写出所需各点的坐标;2.求平面


易错点
1.直线与平面所成的角的公式记错,导致求成
知识点
如图,四边形ABCD中,AB⊥AD,AD∥BC,AD=3,BC=2AB=2,E,F分别在BC,AD上,EF∥AB.现将四边形ABEF沿EF折起,使平面ABEF⊥平面EFDC.
20.若



使得
21.求三棱锥A-CDF的体积的最大值,并求此时二面角E-AC-F的余弦值.
正确答案
(1)
解析
(Ⅰ)因为平面



所以



所以
在折起过程中,


所以
以


若




可得平面

因为
所以
故
则

所以线段



考查方向
解题思路
先根据题中给出的条件证明

易错点
1.不知道折叠前后变的量和不变的量有哪些?2.不会根据题中的条件找到建立坐标系的条件。
正确答案
(2)
解析
(Ⅱ)设


所以
所以当


可得



所以



设平面

则

取

设平面

则
同理可得
所以
所以二面角E﹣AC﹣F的余弦值为
考查方向
解题思路
设出变量后得到函数
易错点
1.不知道折叠前后变的量和不变的量有哪些?2.不会根据题中的条件找到建立坐标系的条件。
如图,












21.求证:
22.求平面

正确答案
(1)略;
解析
解:

而




考查方向
解题思路
先证明
易错点
找不到
正确答案
(2)
解析
设




易知








同理
二面角









考查方向
解题思路
先证明


易错点
找不到二面角的平面角无法做出答案。
如图,五面体





18.求证:直线

19.求二面角
正确答案
略
解析
解:在直角梯形

可得:


又∵


又


可得:
由①②可得:直线

考查方向
解题思路
先证出




易错点
在证明面面垂直时,没有严格按照定理的条件论证,重点是线面垂直,易在过程的严密性上扣分。
正确答案
解析
在直角梯形

可得:


又∵


又


可得:
由①②可得:直线

(Ⅱ)由(Ⅰ)知,建立如图空间直角坐标系,
由题意知各点坐标如下:

因此 
设平面

平面

由
可取
由
可取
于是
故二面角

考查方向
解题思路
(Ⅰ)先证出





易错点
(1).在证明面面垂直时,没有严格按照定理的条件论证,重点是线面垂直,易在过程的严密性上扣分。
(2).建立合理的坐标系,正确求点坐标
如图(1),在等腰梯形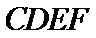
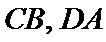

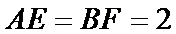
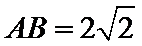
现将梯形沿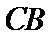
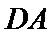
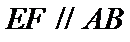
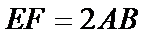
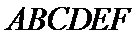
图(2)示,已知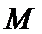
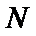
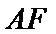
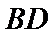
18.求证: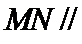
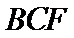
19.若直线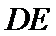
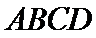
正确答案
见解析
解析
(Ⅰ)证明:连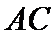
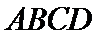
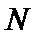
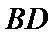
∴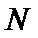
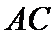
在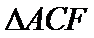
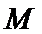
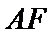
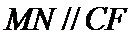
∵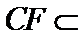
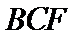
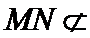
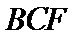
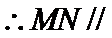
考查方向
解题思路
连结AC,通过证明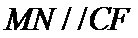
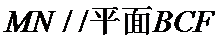
易错点
主要易错于线面角的判断出错,
正确答案
见解析
解析
(Ⅱ)依题意知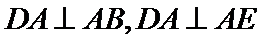
∴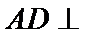
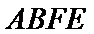
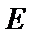
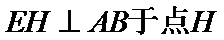
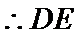
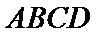
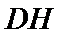
所以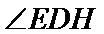
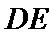
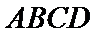
所以:
所以:
设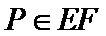
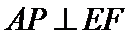
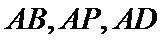

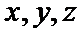
则
设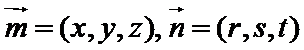
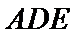
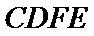
令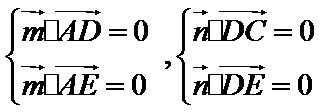
即
取
则
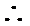
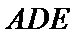
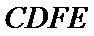
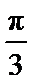
考查方向
解题思路
先由线面垂直的判定定理可证得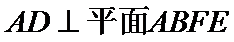
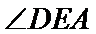
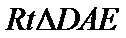
分别以AB,AP,AD所在的直线建立空间直角坐标系,求出平面ADE与平面CDFE的法向量,代入向量夹角公式,可得答案.
易错点
主要易错于线面角的判断出错,
如图,已知在直四棱柱(侧棱垂直底面的棱柱)



21.求证:

22.求

23.求二面角
正确答案
(1)略;
解析
以




则






又因为
所以,

考查方向
解题思路
建立空间直角坐标系,写出所需要的各个点的坐标,然后即可证明,
易错点
在建立坐标系时坐标写错;
正确答案
(2)
解析
(Ⅱ)设

由

得


又
设



即


考查方向
解题思路
先求平面
易错点
记错公式导致结果出错,主要是求正弦余弦弄不明白。
正确答案
(3)
解析
(Ⅲ)由(Ⅱ)知平面
设

由


得


设



所以二面角

考查方向
解题思路
分别求平面

易错点
无
如图4,已知四棱锥P—ABCD中,PA⊥平面ABCD,底面ABCD
中,∠A=90°,AB∥CD,AB=1,AD=CD=2.
22.若二面角P—CD—B为45°,求证:平面

23.在(Ⅰ)的条件下,求点A到平面PBC的距离.
正确答案
(1)略;
解析
Ⅰ)
∵AB//CD,AB⊥AD,∴


∴

取PD的中点E,PC的中点F,连结AE,BF,EF,
则


∴





∴四边形ABFE为平行四边形,∴


∵


考查方向
解题思路
1.先找出


易错点
不会从图形中找到二面角P—CD—B的平面角;
不知道该证明哪条直线垂直于哪个平面;
正确答案
(2)
解析
(Ⅱ)设点A到平面PBC的距离为



考查方向
解题思路
1.先找出


2.利用等体积法直接求解答案即可。
易错点
利用等体积法运算时求解算数出错。
如图,在三棱柱ABC-A1B1C1中,△ABC是边长为2的等边三角形,AA1⊥平面ABC,点E是AB的中点,CE∥平面A1BD。
21.求证:点D是CC1的中点;
22.若A1D⊥BD,求平面A1BD与平面ABC所成二面角(锐角)的余弦值。
正确答案
略
解析
取A1B1的中点F,连接F
由作图过程易得:四边形CEFC1为平行四边形,EC∥AA1。
在△AA1B中,点E是AB的中点,∴点G是A1B的中点,



又CE∥平面A1BD,CE平面EFC1C,
且平面EFC1C平面A1BD=DG,
∴DG∥CE,又∵EG∥CD
∴四边形CEGD为平行四边形,CD=EG=
∴点D是CC1的中点……………………………6
考查方向
解题思路
利用题中条件,证明四边形CEFC1为平行四边形,进而由CE∥平面A1BD。证明得出
易错点
在证明线面垂直时,没有严格按照定理的三个条件去证,重点是线线平行。易在过程的严密性上扣分。
正确答案
解析
由(Ⅰ)知EF∥AA1,AA1⊥平面ABC,
∴EF⊥平面ABC
又△ABC是边长为2的等边三角形,点E是AB的中点,
∴CE⊥AB且CE=
如图,建立空间直角坐标系E-xyz,设EF=2h,…………………7
则B(1,0,0),C(0,




由A1D⊥BD可知:

由z轴⊥平
设平面A1BD的法向量为
由

令x=

∴cos<


∴平面A1BD与平面ABC所成二面角(锐角)的余弦值为
考查方向
解题思路
如图,建立空间直角坐标系E-xyz,设EF=2h,找到两个面的法向量,以下按求二面的步骤就可解。
易错点
建立合理的坐标系,正确求点坐标
8.如图,在长方体








正确答案
解析
设直角三棱锥C-C’PQ的高为h, CQ=x,CP=y,根据直角三棱锥的性质可知,

















考查方向
解题思路
设CQ=x,CP=y, 根据直角三棱锥的性质



易错点
直角三棱锥的重要性质应用不熟
知识点
已知四棱锥P-ABCD的三视图如下图所示,E是侧棱PC上的动点.
是否不论点E在何位置,都有BD⊥AE?证明你的结论;
若
正确答案
略(具体过程看解析);
解析
试题分析:本题属于立体几何中的基本问题,题目的难度是逐渐由易到难,由线面垂直去证明线线垂直; 不论点E在何位置,都有BD⊥AE.
证明如下:由三视图可知,四

∴BD⊥PC.又∵AC∩
都有AE⊂平面PAC.∴不论点E在何位置,都有BD⊥AE.
考查方向
解题思路
本题考查了证明线线垂直,空间向量在立体几何中的应用,解题步骤如下:根据题设应该由线面垂直去证明线线垂直。
易错点
对线线垂直转化为线面垂直的思路受阻;
正确答案
解析
试题分析:本题属于立体几何中的基本问题,题目的难度是逐渐由易到难,建好空间直角坐标系后,求出各点坐标,再求出法向量再算出夹角(亦可用传统法进行求解)。
解法1:在平面DAE内过点D作DF⊥AE于F,连结BF.
∵AD=AB=1,
∴Rt△ADE≌Rt△ABE,从而△AD
∴∠DFB为





解法2:如图,以点C为原点,CD,CB,CP所在的直线分别为x,y,z轴建立空间直角坐标系。则D(1,0,0),A(1,1,0),B(0,1,0),E(0,0,1),
从而



设平面ADE和平面ABE的法向量分别为

由
由


∴θ=


考查方向
解题思路
本题考查了证明线线垂直,空间向量在立体几何中的应用,解题步骤如下:建系,求出对应两个半平面的法向量,再由法向量的方面确定其夹角与二面角的关系。
易错点
二面角与法向量夹角之间是相等还是互补的判断。
扫码查看完整答案与解析