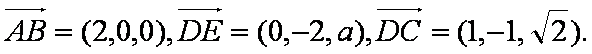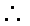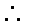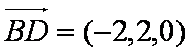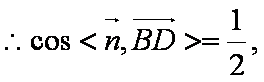- 线面角和二面角的求法
- 共279题
如图,在多面体





(1)求证:

(2)求二面角
正确答案
见解析
解析
(1)取



















又

故












(2)




由勾股定理可得:





由勾股定理可得:

故以








设面



设面

则


所以
设二面角

所以
知识点
将圆


(1)写出直线
(2)求

正确答案
见解析。
解析
(1)直线


(2)设曲线

它到直线



∴当

解法二 ;用直角坐标方程,先求与l平行且与曲线C相切的切线方程,再求平行线间的距离也可(略)
知识点
如图,四棱锥








(1)证明:

(2)求平面

正确答案
见解析
解析
证明:
(1)取





∴



∴









∴




∵





∴

(2)解法一:
连接

建立如图所示的空间直角坐标系,设
则点



设平面




所以平面

所以平面

所以
解法二:
延长



过





令



交




过




所以
所以

知识点
如图,已知四棱锥










(1)证明:平面

(2)求平面

正确答案
见解析。
解析
(1) 证明:



则





(2) 『解法1』:
延长













易求



所以所求角为
因此平面

『解法2』:
以








则





所以

可求得平面
又

可求得平面
则
因此平面


知识点
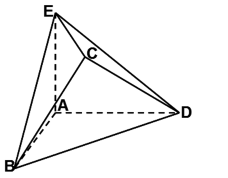
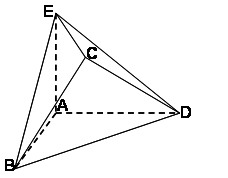
在几何体ABCDE中,AB=AD=BC=CD=2, 
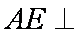
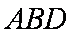
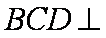
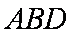
(1)当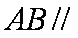
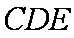
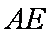
(2)当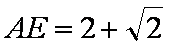
正确答案
见解析
解析
解:(1)设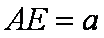
则A(0,0,0),B(2,0,0),D(0,2,0),E(0,0,a),
取BD的中点T,连接CT,AT,则CT
又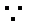
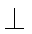
所以CT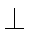
所以CT//AE.
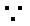

所以CD
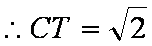
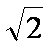
设平面CDE的法向量为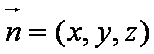
则有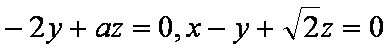
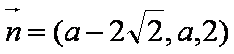
即AE的长为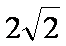
(2)连接AC,当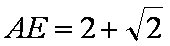
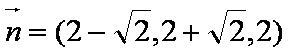
又BD
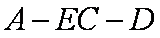
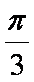
知识点
某高速公路收费站入口处的安全标识墩如图4所示,墩的上半部分是正四棱锥P—EFGH,下半部分是长方体ABCD—EFGH,图5、图6分别是该标识墩的正(主)视图和俯视图。
(1)请画出该安全标识墩的侧(左)视图;
(2)求该安全标识墩的体积;
(3)证明:直线BD⊥平面PEG
正确答案
见解析
解析
(1)侧视图同正视图,如下图所示。
(2)该安全标识墩的体积为:
=
(3)如图,连结EG,HF及BD,EG与HF相交于O,连结PO,
由正四棱锥的性质可知,PO⊥平面EFGH,∴PO⊥HF
又EG⊥HF ∴HF⊥平面PEG
又BD∥HF ∴BD⊥平面PEG
知识点
如图,已知矩形






(1)求证:

(2)求二面角
(3)求多面体
正确答案
见解析
解析
(1)连接



在矩形








(2)由题设易知



则建立如图所示的空间直角坐标系,


设平面

则
取


平面

设二面角




(3)过点






即







知识点
如图所示,直角梯形ACDE与等腰直角


(1)求证:

(2)求二面角
正确答案
见解析
解析
(1)取BD的中点P,连结EP、FP,则PF
又∵EA

∴四边形AFPE是平行四边形,∴AF∥EP,
又∵


∴AF∥面BDE.…………………………………………4分
(2)以CA、CD所在直线分别作为x轴,z轴,以过C点和AB平行的直线作为y轴,建立如图所示坐标系.…………………5分
由
则
∵面




∴

设面


∴



所以n=(1,1,2)是面
故
图形可知二面角


知识点
如图,正方形ABCD所在平面与平面四边形ABEF所在平面互相垂直,△ABE是等腰直角三角形,AB=AE,FA=FE,∠AEF=40°
(1)求证:EF⊥平面B
(2)设线段CD、AE的中点分别为P、M,求证:PM∥平面BCE
(3)求二面角F—BD—A的大小。
正确答案
见解析
解析
(1)证明:因为平面ABEF⊥平面ABCD,BC
所以BC⊥EF。

所以


所以
因为BC

BC∩BE=B
所以EF⊥平面BCE
(2)取BE的中点
∴PMNC为平行四边形,所以PM∥CN。
∵CN在平面BCE内,PM不在平面BCE内。
∴PM//平面BCE。
(3)因△ABE等腰直角三角形,AB=AE,所以AE⊥AB
又因为平面ABEF∩平面ABCD=AB,所以AE⊥平面ABCD,所以AE⊥AD
即AD、AB、AE两两垂直;如图建立空间直解坐标系,
设AB=1,则AE=1,B(0,1,0),D(1,0,0),

设平面BDF的一个法向量为

取y=1,则x=1 ,z=3,从而
取平面ABCD的一个法向量为
故二面角
知识点
在四棱锥P﹣ABCD,PA=PB=AD=AB=4BC=4,E为PB的中点,AD∥BC,且AD⊥面PAB
(1)求证:BD⊥CE
(2)求二面角E﹣AC﹣B的余弦值大小。
正确答案
见解析
解析
解:(1)在四棱锥P﹣ABCD中,由于E为PB的中点,
再取DP的中点F,AP的中点为K,
则FK是三角形PAD的中位线,FK平行且等于
EF是三角形PBD的中位线,故有BD∥EF ①。
再根据PA=PB=AD=AB=4BC=4,AD∥BC,且AD⊥面PAB,
可得EF=



FC=


显然有 CE2+EF2=FC2,∴EF⊥CE ②。
由①、②可得BD⊥CE。
(2)由题意可得平面ABCD⊥平面PAB,过点E作EG⊥AB,G为垂足,则EG⊥平面ABCD。
再过点G作GH⊥AC,H为垂足,则有三垂线定理可得,EH⊥AC,∴∠EHG为二面角E﹣AC﹣B的平面角。
由




由于AD⊥面PAB,AD∥BC,∴BC⊥面PAB,∴CPB⊥面PAB。
再根据等边三角形种AE⊥PB,∴AE⊥平面PBC,∴AE⊥EC。
再根据




直角三角形EGH中,sin∠EHG=

∴cos∠EHG=


知识点
扫码查看完整答案与解析