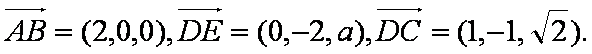- 线面角和二面角的求法
- 共279题
将圆


(1)写出直线
(2)求

正确答案
见解析。
解析
(1)直线


(2)设曲线

它到直线



∴当

解法二 ;用直角坐标方程,先求与l平行且与曲线C相切的切线方程,再求平行线间的距离也可(略)
知识点
如图,四棱锥








(1)证明:

(2)求平面

正确答案
见解析
解析
证明:
(1)取





∴



∴









∴




∵





∴

(2)解法一:
连接

建立如图所示的空间直角坐标系,设
则点



设平面




所以平面

所以平面

所以
解法二:
延长



过





令



交




过




所以
所以

知识点
如图,已知四棱锥










(1)证明:平面

(2)求平面

正确答案
见解析。
解析
(1) 证明:



则





(2) 『解法1』:
延长













易求



所以所求角为
因此平面

『解法2』:
以








则





所以

可求得平面
又

可求得平面
则
因此平面


知识点
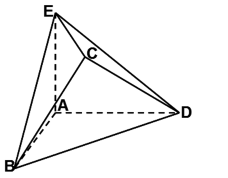
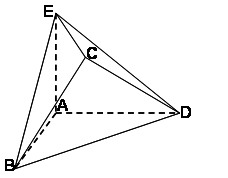
在几何体ABCDE中,AB=AD=BC=CD=2, 
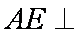
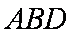
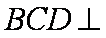
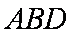
(1)当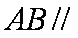
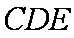
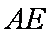
(2)当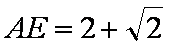
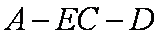
正确答案
见解析
解析
解:(1)设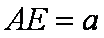
则A(0,0,0),B(2,0,0),D(0,2,0),E(0,0,a),
取BD的中点T,连接CT,AT,则CT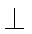
又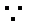
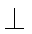
所以CT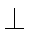
所以CT//AE.
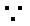

所以CD
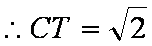
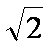
设平面CDE的法向量为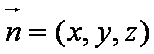
则有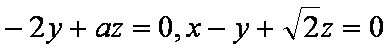
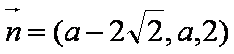
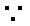
即AE的长为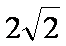
(2)连接AC,当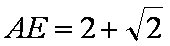
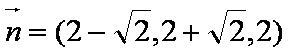
又BD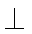
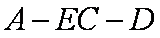
知识点
在四棱锥P﹣ABCD,PA=PB=AD=AB=4BC=4,E为PB的中点,AD∥BC,且AD⊥面PAB
(1)求证:BD⊥CE
(2)求二面角E﹣AC﹣B的余弦值大小。
正确答案
见解析
解析
解:(1)在四棱锥P﹣ABCD中,由于E为PB的中点,
再取DP的中点F,AP的中点为K,
则FK是三角形PAD的中位线,FK平行且等于
EF是三角形PBD的中位线,故有BD∥EF ①。
再根据PA=PB=AD=AB=4BC=4,AD∥BC,且AD⊥面PAB,
可得EF=



FC=


显然有 CE2+EF2=FC2,∴EF⊥CE ②。
由①、②可得BD⊥CE。
(2)由题意可得平面ABCD⊥平面PAB,过点E作EG⊥AB,G为垂足,则EG⊥平面ABCD。
再过点G作GH⊥AC,H为垂足,则有三垂线定理可得,EH⊥AC,∴∠EHG为二面角E﹣AC﹣B的平面角。
由




由于AD⊥面PAB,AD∥BC,∴BC⊥面PAB,∴CPB⊥面PAB。
再根据等边三角形种AE⊥PB,∴AE⊥平面PBC,∴AE⊥EC。
再根据




直角三角形EGH中,sin∠EHG=

∴cos∠EHG=


知识点
扫码查看完整答案与解析