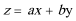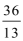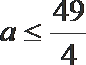- 指数函数的图像变换
- 共416题
17.已知函数f(x)=ax+x2-xln a-b(a,b∈R,a>1),e是自然对数的底数.
(1)试判断函数f(x)在区间(0,+∞)上的单调性;
(2)当a=e ,b=4时,求整数k的值,使得函数f(x)在区间(k,k+1)上存在零点。
正确答案
解:(1)f′(x)=axln a+2x-ln a=2x+(ax-1)ln a.
∵a>1,∴当x∈(0,+∞)时,ln a>0,ax-1>0,
∴f′(x)>0,
∴函数f(x)在(0,+∞)上单调递增.
(2)∵f(x)=ex+x2-x-4,∴f′(x)=ex+2x-1,
∴f′(0)=0,
当x>0时,ex>1,∴f′(x)>0,
∴f(x)是(0,+∞)上的增函数;
同理,f(x)是(-∞,0)上的减函数.
又f(0)=-3<0,f(1)=e-4<0,f(2)=e2-2>0,
当x>2时,f(x)>0,
∴当x>0时,函数f(x)的零点在(1,2)内,
∴k=1满足条件;
f(0)=-3<0,f(-1)=-2<0,
f(-2)=+2>0,
当x<-2时,f(x)>0,
∴当x<0时,函数f(x)的零点在(-2,-1)内,
∴k=-2满足条件.
综上所述,k=1或-2.
解析
解析已在路上飞奔,马上就到!
知识点
6.已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.如图,已知半椭圆


(I)求a的值及直线l的方程(用x0,y0表示);
(II)△OAB的面积是否存在最大值?若存在,求出最大值;若不存在,说明理由.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.在△ABC中,

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.一袋子中有大小、质量均相同的10个小球,其中标记“开”字的小球有5个,标记“心”字的小球有3个,标记“乐”字的小球有2个.从中任意摸出1个球确定标记后放回袋中,再从中任取1个球.不断重复以上操作,最多取3次,并规定若取出“乐”字球,则停止摸球.则摸球次数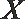
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.已知向量




(Ⅰ)求
(Ⅱ)在△ABC中,


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.下图是2014年在某大学自主招生面试环节中,七位评委为某考生打出的分数的茎叶图,则去掉一个最高分和一个最低分后,所剩数据的平均数和方差分别为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.设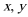
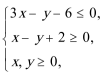
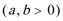
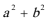
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知







正确答案
18π
解析
解析已在路上飞奔,马上就到!
知识点
17.已知函数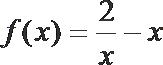
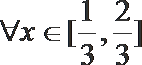
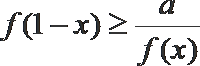
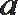
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析