- 指数函数的图像变换
- 共416题
在如图所示的空间直角坐标系

正确答案
解析
略
知识点
(本小题满分12分)
设等差数列{an}的前n项和为Sn, 且a1=3,S5-S2=27,
(1)求数列an的通项公式
(2)若
正确答案
(1)
解析
(1)设等差数列

则
又


(2)由(1)可得

即

解得


知识点
定义两个平面向量的一种运算
正确答案
解析
A显然成立;对于B,λ(a⊗b)=λ|a|·|b|sin〈a,b〉,(λa)⊗b=|λa|·|b|sin〈a,b〉,当λ<0时,λ(a⊗b)=(λa)⊗b不成立;对于C,由a⊗b=|a|·|b|sin〈a,b〉,a·b=|a|·|b|cos〈a,b〉,可知(a⊗b)2+(a·b)2=|a|2·|b|2;对于D,(a⊗b)2=|a|2·|b|2-(a·b)2=(x1(2)+y1(2))(x2(2)+y2(2))-(x1x2+y1y2)2=(x1y2-x2y1)2,故a⊗b=|x1y2-x2y1|恒成立。
知识点
已知函数
(1)若函数
(2)令


(3)当
正确答案
见解析
解析
(1)
令


所以
(2)假设存在实数a,使

①当

②当


所以
③当

综上,存在实数

(3)令



当



所以
所以

知识点
已知锐角三角形



(1) 求角
(2) 求

正确答案
(1)
解析
(1)由余弦定理得 
(2)
=

知识点
已知函数
(1)求
(2)求
正确答案
(1)
解析

=

(1)
(2)令
即



知识点
设



(1)求实数

(2)设



(3)若正实数







正确答案
见解析
解析
本题考查运用导数知识研究函数的图象与性质、函数的应用、不等式问题、数学归纳法等基础知识,考查运算求解能力、推理论证能力,考查数形结合思想、函数与方程思想、特殊与一般思想等.
(1)∵


令



所以


(2)由

令函数





而

所以
(3)证明:不妨设

其中

令









从而有
该不等式能更进一步推广:
已知




下面用数学归纳法加以证明:
i)当
ii)假设当

则当



在该不等式的两边同时乘以正数

在此不等式的两边同时加上

该不等式的左边再利用i)的结论可得:

所以,当
综上,对
知识点
观察下列不等式
①

则第5个不等式为
正确答案
解析
略
知识点
. f(x)=
(1)求证: 
(2)若不等式


正确答案
见解析
解析
(1)证明:


当



即

(2)解法一:由(1)知



设











又





当











综上,实数

解法二:因为
设
则
可求
所以当



所以

所以


当





此时一定有



综上所述,


知识点
已知函数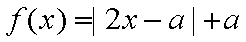
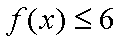
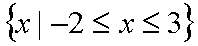
(1)求实数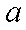
(2)若存在实数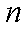
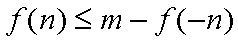
正确答案
见解析
解析
(1)
又∵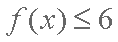
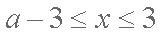
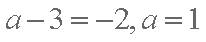
(2)由(1)知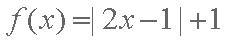
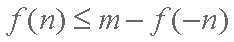
∴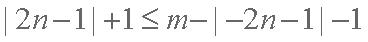
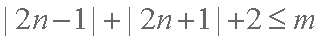
又∵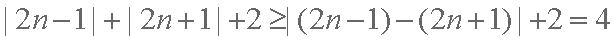
∴
知识点
扫码查看完整答案与解析