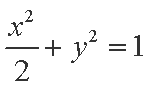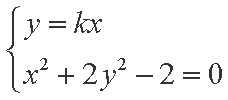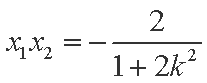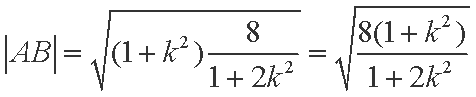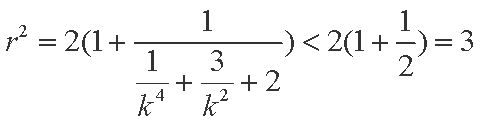- 指数函数的图像变换
- 共416题
已知抛物线C:
(1) 若
(2)问在抛物线C上是否存在定点N(x0,y0),使得NA⊥NB总成立,若存在,求出N点的坐标,若不存在,请说明理由
正确答案
见解析
解析
(1)当



则






(2)设在抛物线上存在定点

















由此可得:①当




知识点
已知椭圆






(1)求椭圆的方程;
(2)若






(3)在(2)的条件下,试问



正确答案
见解析。
解析
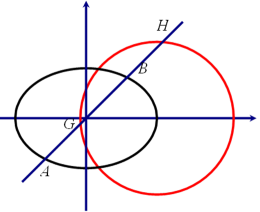
(1)如图,由题意得,

所求的椭圆方程为
(2)由(1)知,


由题意可设







由 




即
(3)设
若以




由(2)可知

即





知识点
设公比大于零的等比数列










(1)求数列

(2)设


正确答案
见解析
解析
(1)由


又

则得
所以

(2)


则

即

当



知识点
设函数
(1)求
(2)若


正确答案
见解析
解析
(1)设函数



(2)∵
∴
∴
知识点
已知圆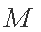
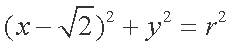


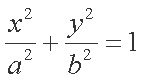

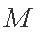
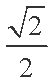
(1)求椭圆
(2)若存在直线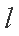
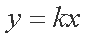
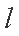

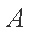
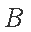
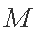

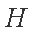

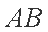
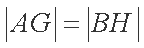
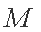
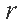
正确答案
见解析
解析
(1)设椭圆的焦距为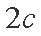
因为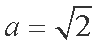
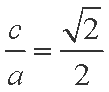
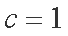
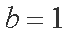

(2)设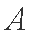

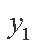
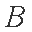
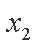
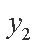
由直线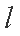

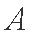
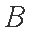
所以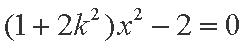

所以
点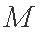
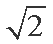
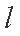
则
显然,若点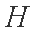
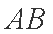
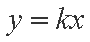
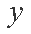
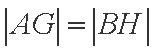
所以
当

当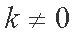
又显然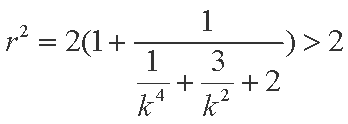
综上,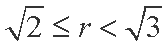
知识点
扫码查看完整答案与解析