坐标系与参数方程
共275题

坐标系与参数方程
共275题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 5 分

15. 在直角坐标系X0Y中，以原点O为极点，X轴的正半轴为极轴建立极坐标系. 极坐标方程为的直线与曲线（为参数）相交于A,B两点, 则_______

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

直线与圆相交的性质参数方程化成普通方程直线的参数方程圆的参数方程

题型：填空题

填空题 · 5 分

13．极坐标系与直角坐标系有相同的长度单位，以原点为极点，以轴正半轴为极轴.已知直线的参数方程为（为参数），曲线的极坐标方程为.设直线与曲线交于两点，

弦长___________

正确答案

解析

ρsin2θ=8cosθ

ρ2sin2θ=8ρcosθ

y2=8x

联立可得：3x2-20x+12=0

所以弦长|AB|=x1+x2+p=

考查方向

参数方程，圆锥曲线

解题思路

参数方程化为一般方程，直线与抛物线相交，弦长公式进行计算。

易错点

曲线方程与参数方程联立计算容易出错，没弄清参数方程的集合意义。

教师点评

本题难度不大，关键得熟练的掌握参数方程与普通方程的互化。

知识点

简单曲线的极坐标方程参数的意义直线的参数方程

题型：填空题

填空题 · 5 分

13．直线：（为参数），圆：（极轴与x轴的非负半轴重合，且单位长度相同），若圆上至少有三个点到直线的距离恰为，则实数的取值范围为_________．

正确答案

解析

由题可知，直线方程为：2x+ay=a，圆的方程(x-1)2+(y-1)2=2，圆心到直线的距离不大于，利用点到直线的距离公式，解得：a∈

考查方向

本题主要考查极坐标系和参数方程

解题思路

1、转化为普通方程；2、画图求解，即可得到结果。

易错点

本题易在转化为普通方程时发生错误。

知识点

直线与圆的位置关系简单曲线的极坐标方程直线的参数方程

题型：简答题

简答题 · 7 分

已知曲线C1：（为参数），曲线C2：（t为参数）。

（1）指出C1，C2各是什么曲线，并说明C1与C2公共点的个数；

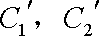
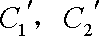
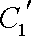
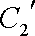
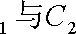
（2）若把C1，C2上各点的纵坐标都压缩为原来的一半，分别得到曲线，写出的参数方程。与公共点的个数和C公共点的个数是否相同？说明你的理由。

正确答案

见解析

解析

（1）是圆，是直线。

的普通方程为，圆心，半径。

的普通方程为。 ……………2分

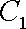
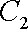
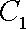
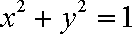
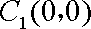
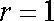
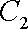
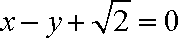
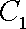
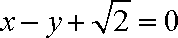
因为圆心到直线的距离为，

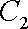
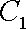
所以与只有一个公共点。 ……………4分

（2）压缩后的参数方程分别为

：（为参数）；：（t为参数）。

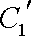
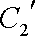
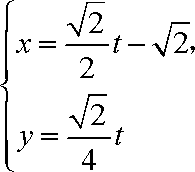
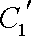
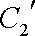
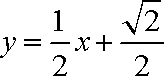
化为普通方程为：：，：，……………6分

联立消元得，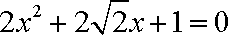

其判别式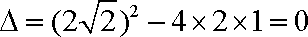，……………7分

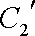
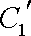
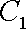
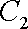
所以压缩后的直线与椭圆仍然只有一个公共点，和与公共点个数相同。

知识点

直线与圆的位置关系参数方程化成普通方程直线的参数方程圆的参数方程

题型：简答题

简答题 · 10 分

以直角坐标系的原点为极点O，轴正半轴为极轴，已知点P的直角坐标为(1,5),点C的极坐标为,若直线L经过点P,且倾斜角为，圆C的半径为4.

（1）求直线l的参数方程及圆C的极坐标方程；

（2）试判断直线l与圆C有位置关系.

正确答案

见解析。

解析

（1）直线的参数方程，即（为参数）

由题知点的直角坐标为，圆半径为，

∴圆方程为将代入

得圆极坐标方程 ………5分

（2）由题意得，直线的普通方程为，

圆心到的距离为，

∴直线与圆相离。 ………10分

知识点

直线与圆的位置关系简单曲线的极坐标方程点的极坐标和直角坐标的互化直线的参数方程

题型：简答题

简答题 · 10 分

已知直线为参数), 曲线（为参数）.

（1）设与相交于两点,求；

（2）若把曲线上各点的横坐标压缩为原来的倍,纵坐标压缩为原来的倍,得到曲线,设点是曲线上的一个动点,求它到直线的距离的最小值。

正确答案

见解析

解析

（1）的普通方程为的普通方程为

联立方程组解得与的交点为,,则.

（2）的参数方程为为参数)。故点的坐标是,

从而点到直线的距离是,

由此当时,取得最小值,且最小值为.

知识点

函数的图象与图象变化直线与圆相交的性质参数方程化成普通方程直线的参数方程圆的参数方程

题型：简答题

简答题 · 10 分

在平面直角坐标系xOy中，已知直线l的参数方程为(t为参数)，直线l与抛物线交于两点，求线段AB的长。

正确答案

见解析。

解析

直线l：代入抛物线方程并整理得

∴交点，，故

知识点

直线与抛物线的位置关系直线的参数方程

题型：简答题

简答题 · 10 分

在直角坐标系中，已知点，直线的参数方程是

（为参数），以为极点，轴正半轴为极轴建立极坐标系，圆的极坐标方

程是。

（1）将圆的极坐标方程化为直角坐标方程，并写出圆心的极坐标

（2）若直线与圆交于两点，求的值。

正确答案

见解析

解析

解：（1）∵，

∴ ，∴，

∴圆的直角坐标方程为：，

圆心的直角坐标为，极坐标为；

（2）直线的参数方程可写为：（为参数），

代入圆的直角坐标方程中得：，

设两点所对应的参数分别为，则，

∴。

知识点

直线与圆相交的性质简单曲线的极坐标方程点的极坐标和直角坐标的互化直线的参数方程

题型：填空题

填空题 · 5 分

13．直线为参数）上与点的距离等于的点的坐标是____________.

正确答案

或

解析

解析已在路上飞奔，马上就到！

知识点

点到直线的距离公式直线的参数方程

题型：填空题

填空题 · 5 分

9．若直线与直线（为参数）垂直，则（）．

正确答案

− 1

解析

解析已在路上飞奔，马上就到！

知识点

两条直线垂直与倾斜角、斜率的关系直线的参数方程

继续学习学习下一知识点

下一知识点 : 不等式选讲

百度题库 > 高考 > 理科数学 > 坐标系与参数方程

扫码查看完整答案与解析