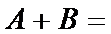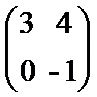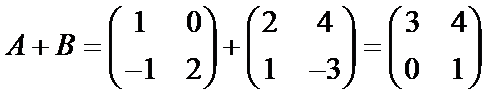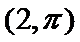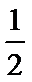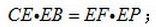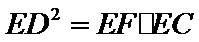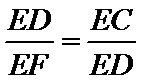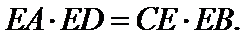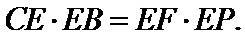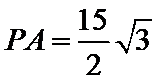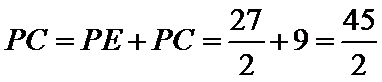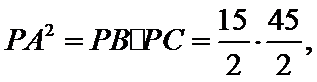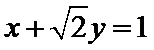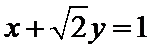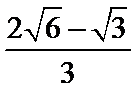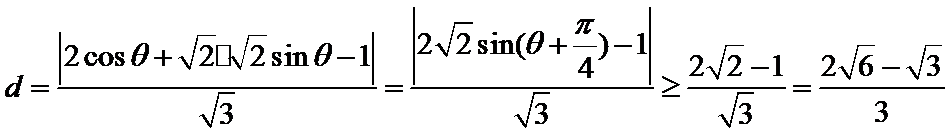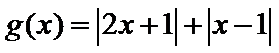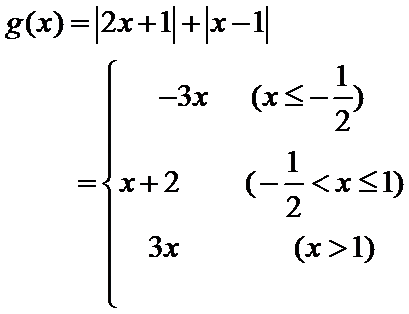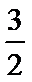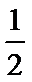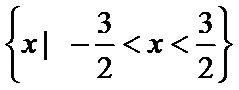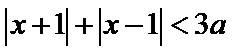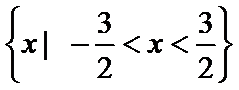- 坐标系与参数方程
- 共275题
11.在极坐标系中,直线


正确答案
2
知识点
22.(2) [选修4-4:坐标系与参数方程]
在直角坐标系








(1)求

(2)若






正确答案
见解析
解析
(1)
(2)曲线






所以
当


考查方向
解题思路
(1)利用已知条件把

(2)把
易错点
本题必须注意把

知识点
1. 已知矩阵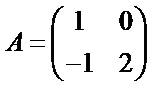
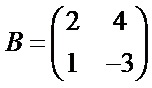
正确答案
解析
因为A,B两个矩阵的维数相同,A+B即将它们各位置上的元素相加即可。
考查方向
解题思路
本题主要考查了矩阵加减运算,直接按照运算法则计算即可。
易错点
本题必须注意 当两个矩阵A,B的维数相同时,将它们各位置上的元素加(减)所得到的矩阵称为矩阵A,B的和(差),记作:A+B(A-B)
知识点
15.已知直线l的参数方程为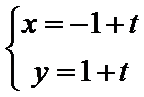
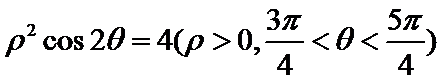
正确答案
解析
直线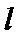
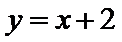
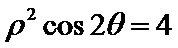
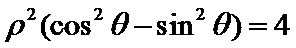
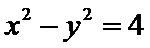
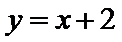
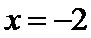
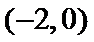
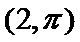
考查方向
解题思路
参数方程主要通过代入法或者已知恒等式(如
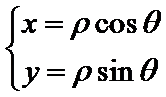
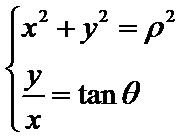
易错点
参数方程与普通方程的转化
知识点
正确答案
LUE
知识点
22.选修4-4:坐标系与参数方程
在极坐标系中,已知圆C的圆心
(1)求圆C的极坐标方程;
(2)若点Q在圆C上运动,P在OQ的延长线上,且|OQ|∶|QP|=3∶2,求动点P的轨迹方程.
正确答案
(1)
(2)
解析
试题分析:本题属于坐标系与参数方程中的基本问题,题目的难度一般,解题过程如下:
(1)设



∵


∴


(2)设点










考查方向
解题思路
本题考查极坐标方程的知识,可以根据求圆的极坐标方程所需的条件寻求关系。
易错点
没有准确理解极坐标下的轨迹方程而导致本题不会做。
知识点
13.极坐标系与直角坐标系










弦长
正确答案
解析
ρsin2θ=8cosθ
ρ2sin2θ=8ρcosθ
y2=8x
联立可得:3x2-20x+12=0
所以弦长|AB|=x1+x2+p=
考查方向
参数方程,圆锥曲线
解题思路
参数方程化为一般方程,直线与抛物线相交,弦长公式进行计算。
易错点
曲线方程与参数方程联立计算容易出错,没弄清参数方程的集合意义。
教师点评
本题难度不大,关键得熟练的掌握参数方程与普通方程的互化。
知识点
13.直线








正确答案
解析
由题可知,直线方程为:2x+ay=a,圆的方程(x-1)2+(y-1)2=2,圆心到直线的距离不大于
考查方向
解题思路
1、转化为普通方程;2、画图求解,即可得到结果。
易错点
本题易在转化为普通方程时发生错误。
知识点
选修44:坐标系与参数方程
正确答案
解析
知识点
请考生在以下三题中任选一题作答,如果多做,则按所做的第一题记分.作答时用2B铅笔在答题卡上把所选题目对应的题号涂黑.
【选修4—1】几何证明选讲(请回答28、29、30题)
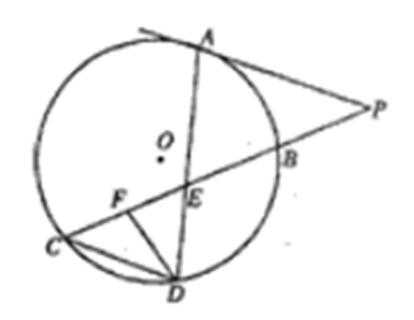
如图:已知PA切圆O于A,PBC是割线,弦CD∥AP,AD交BC于E,F在CE上,且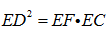
【选修4—4】坐标系与参数方程(请回答31、32题)
在直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴建立极坐标系。已知曲线C1的极坐标方程为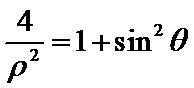
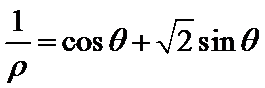
【选修4—5】不等式选讲(请回答33、34题)
已知函数
28.求证:∠EDF=∠P;
29.求证:
30.若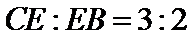
31.写出曲线C1与直线l的直角坐标方程;
32.设Q为曲线C1上一动点,求Q点到直线l距离的最小值。
33.求a的值;
34.解不等式:
正确答案
证明:∵
∴
又∵∠DEF=∠CED
∴△DEF∽△CED
∴∠C=∠EDF 又CD∥AP,
∴∠C=∠P.
∴∠EDF=∠P.
解析
证明:∵
∴
又∵∠DEF=∠CED
∴△DEF∽△CED
∴∠C=∠EDF 又CD∥AP,
∴∠C=∠P.
∴∠EDF=∠P.
考查方向
解题思路
先证明△DEF∽△CED,再根据平行求出∠EDF=∠P.
易错点
切割线定理在应用的时候出错,线段成比例找不对容易出错,相似三角形不写成对应的容易导致比例线段出错。
正确答案
证明:
由(1)得∠EDF=∠P,又∠FED=∠PEA,
∴△FED∽△AEP. ∴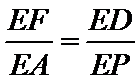
∴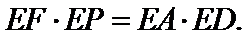
∴
解析
证明:
由(1)得∠EDF=∠P,又∠FED=∠PEA,
∴△FED∽△AEP. ∴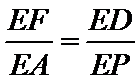
∴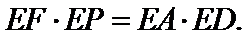
∴
考查方向
解题思路
借助第一问,求得△FED∽△AEP,进而得出成比例线段。
易错点
切割线定理在应用的时候出错,线段成比例找不对容易出错,相似三角形不写成对应的容易导致比例线段出错。
正确答案
解析
证明:
设CE=3k,EB=2k.
∵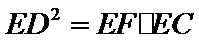
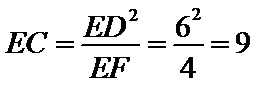
又CE=3k=9, k=3,EB=2k=6.
由(2)得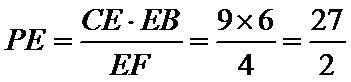
故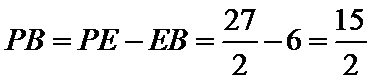
∵
∴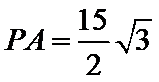
考查方向
解题思路
借助第一二问,根据成比例线段得出结果。
易错点
切割线定理在应用的时候出错,线段成比例找不对容易出错
正确答案
C1的直角坐标方程: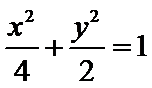
解析
根据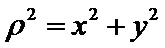
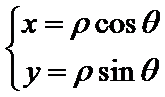
C1的直角坐标方程: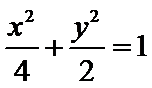
考查方向
解题思路
根据极坐标与直角坐标互化的公式可以直接得到曲线C1与直线l的直角坐标方程;
易错点
极坐标与直角坐标的转化
正确答案
解析
由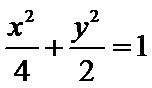
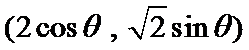
∴点Q到直线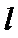
考查方向
解题思路
将曲线C1的直角坐标方程转化为参数方程,代入点Q到直线的距离公式,利用三角恒等变换得到最值。
易错点
点到直线距离公式的应用,计算出错。
正确答案
a=1
解析
可以先不考虑参数a,令
画出图形,即可知道函数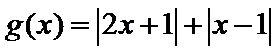
因为函数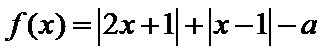
所以a=1
【三级考点】不等式的基本性质,绝对值不等式的解法
考查方向
解题思路
利用零点分段法解绝对值不等式,讨论三种情况。
易错点
在对函数的最小值进行求解时,参数的处理容易出错
正确答案
解析
把a=1代入
利用零点分段法可以得到此不等式的解集是
考查方向
解题思路
利用零点分段法解绝对值不等式,讨论三种情况。
易错点
解决第二问的时候,要注意不等式的最小值。
扫码查看完整答案与解析