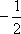平面向量数量积的运算
共301题

· 平面向量数量积的运算

平面向量数量积的运算
共301题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 20 分

请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。

正确答案

测试

题型：填空题

填空题 · 20 分

请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。

正确答案

测试

题型：填空题

填空题 · 4 分

设为单位向量，非零向量，若的夹角为，则的最大值等于________。

正确答案

解析

由已知得到：，设的最大值为4，所以答案是2

知识点

平面向量的基本定理及其意义平面向量数量积的运算数量积表示两个向量的夹角

题型：填空题

填空题 · 5 分

在平行四边形ABCD中，AD＝1，∠BAD＝60°，E为CD的中点，若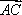·＝1，则AB的长为__________。

正确答案

解析

如图所示，在平行四边形ABCD中，＝＋，＝＋＝＋.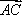

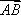
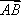
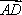
所以·＝（＋）·＝||2＋||2＋·＝||2＋||＋1＝1，解方程得||＝（舍去||＝0），所以线段AB的长为.

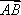
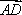
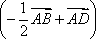
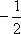
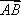
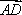
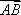
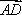
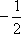
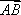
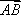
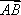
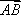
知识点

平面向量数量积的运算向量在几何中的应用

题型：填空题

填空题 · 4 分

在ABC中，M是BC的中点，AM＝3，BC＝10，则＝______________。

正确答案

解析

此题最适合的方法是特例法。

假设ABC是以AB＝AC的等腰三角形，如图，

AM＝3，BC＝10，AB＝AC＝。

cos∠BAC＝。＝

知识点

平面向量数量积的运算向量在几何中的应用

题型：填空题

填空题 · 4 分

若平面向量α，β满足|α|≤1，|β|≤1，且以向量α，β为邻边的平行四边形的面积为，则α与β的夹角的取值范围是。

正确答案

解析

由题意得：，∵，，∴，

又∵，∴.

知识点

平面向量数量积的运算数量积表示两个向量的夹角向量在几何中的应用

题型：填空题

填空题 · 4 分

如图，在中，,,,则 .

正确答案

解析

本题主要考查平面向量的基本运算与解三角形的基础知识，属于难题。

知识点

平面向量数量积的运算向量在几何中的应用

题型：单选题

单选题 · 5 分

若点O和点分别是双曲线的中心和左焦点,点P为双曲线右支上的任意一点,则的取值范围为 ( )

正确答案

解析

因为是已知双曲线的左焦点，所以，即，所以双曲线方程为，设点P，则有，解得，因为，，所以=，此二次函数对应的抛物线的对称轴为，因为，所以当时，取得最小值，故的取值范围是

知识点

平面向量数量积的运算双曲线的几何性质

题型：单选题

单选题 · 5 分

在中，，，，则

正确答案

解析

由下图知.

.又由余弦定理知，解得.

知识点

平面向量数量积的运算向量在几何中的应用

题型：填空题

填空题 · 5 分

已知点为等边三角形的中心,,直线过点交边于点，交边于点，则的最大值为

正确答案

解析

试题分析：以M点为原点，x轴平行于,y轴垂直于，建立直角坐标系，则M（0，0），A（0，）,B（-1，-）,C（1，-），

设直线l的方程为y=kx （0≤k≤）（1），直线AB的方程y-=（2），

联立（1）（2），得P点的坐标为（，），

直线AC的方程：y-=-x，（3），

联立（1）（3），得Q点的坐标为（，），

则=（+1，+）,

即=（+1，），=（-1，）,

·=（+1）（-1）+（）（）=，

因为0≤k≤，所以·=≤=，

当且仅当k=0，即直线l平行于x轴时取等号。

故·的最大值是.

知识点

平面向量数量积的运算向量在几何中的应用

继续学习学习下一知识点

下一知识点 : 数量积表示两个向量的夹角

百度题库 > 高考 > 理科数学 > 平面向量数量积的运算

扫码查看完整答案与解析