- 两条直线平行与倾斜角、斜率的关系
- 共51题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
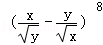
正确答案
70
解析
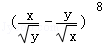
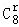
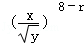
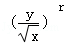
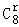
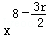

令 8﹣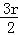
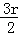
故展开式中x2y2的系数为 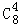
故答案为:70。
知识点
若函数y=logax(a>0,且a≠1)的图象如图所示,则下列函数图象正确的是( )
正确答案
解析
函数的性质及应用。
由题意可得a=3,由基本初等函数的图象和性质逐个选项验证即可。
由题意可知图象过(3,1),
故有1=loga3,解得a=3,
选项A,y=a﹣x=3﹣x=
选项B,y=x3,由幂函数的知识可知正确;
选项C,y=(﹣x)3=﹣x3,其图象应与B关于x轴对称,故错误;
选项D,y=loga(﹣x)=log3(﹣x),当x=﹣3时,y=1,
但图象明显当x=﹣3时,y=﹣1,故错误。
知识点
△ABC的内角A、B、C的对边分别为a、b、c,已知3acosC=2ccosA,tanA=
正确答案
B=
解析
∵3acosC=2ccosA,
由正弦定理可得3sinAcosC=2sinCcosA,
∴3tanA=2tanC,
∵tanA=
∴2tanC=3×

∴tanB=tan[π﹣(A+C)]=﹣tan(A+B)=﹣

∵B∈(0,π),
∴B=
知识点
直线


正确答案
2
解析
方法一、圆心为(0,0),半径为2
圆心到直线
故
得|AB|=2
知识点



正确答案
解析
A答案还有异面或者相交,C、D不一定
知识点
如图,半径为R的球O中有一内接圆柱,当圆柱的侧面积最大是,求的表面积与改圆柱的侧面积之差是 。
正确答案
解析


知识点
如图









给出下列三个结论:
①
②
③
正确答案
解析
①正确,由条件可知,BD=BF,CF=CE,可得
②正确,通过条件可知,AD=AE,由切割定理可得
③错误,连接FD(如下图),若


知识点
甲、乙、丙三人进行羽毛球练习赛,其中两人比赛,另一人当裁判,每局比赛结束时,负的一方在下一局当裁判,设各局中双方获胜的概率均为
(1)求第4局甲当裁判的概率;
(2)X表示前4局中乙当裁判的次数,求X的数学期望。
正确答案
见解析。
解析
(1)记A1表示事件“第2局结果为甲胜”,
A2表示事件“第3局甲参加比赛时,结果为甲负”,A表示事件“第4局甲当裁判”。
则A=A1·A2.
P(A)=P(A1·A2)=P(A1)P(A2)=
(2)X的可能取值为0,1,2.
记A3表示事件“第3局乙和丙比赛时,结果为乙胜丙”,B1表示事件“第1局结果为乙胜丙”,B2表示事件“第2局乙和甲比赛时,结果为乙胜甲”,B3表示事件“第3局乙参加比赛时,结果为乙负”。
则P(X=0)=P(B1·B2·A3)=P(B1)P(B2)·P(A3)=





知识点
扫码查看完整答案与解析





































