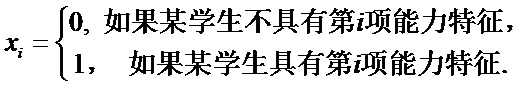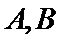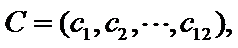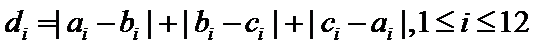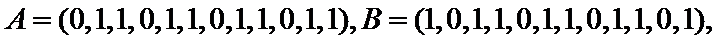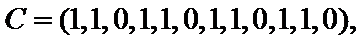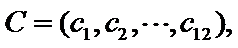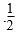- 计数原理
- 共551题
用数字1,2,3,4,5组成没有重复数字的五位数,其中奇数的个数为
正确答案
知识点
设(1-x)n=a0+a1x+a2x2+…+anxn,n∈N*,n≥2.
33.设n=11,求|a6|+|a7|+|a8|+|a9|+|a10|+|a11|的值;
34.设bk=

正确答案
(1)1024;
解析
解:(1)因为ak=(-1)k 
当n=11时,|a6|+|a7|+|a8|+|a9|+|a10|+|a11|=
=
考查方向
解题思路
本题考查二项式定理和性质,解题步骤如下:
(1)由二项式定理可得ak=(-1)k
=(-1)k-1 

易错点
二项式定理和性质不会熟练应用,容易计算错误
正确答案
(2)1
解析
(2)bk=


当1≤k≤n-1时,bk=(-1)k+1 





当m=0时,|

当1≤m≤n-1时,
Sm=-1+

所以|

考查方向
解题思路
本题考查二项式定理和性质,解题步骤如下:
(2)由组合数的阶乘公式可得bk= (-1)k+1 
=(-1)k-1 

易错点
二项式定理和性质不会熟练应用,容易计算错误
13. 已知正四面体










正确答案
9
解析
设正四面体的棱长为2;
(1)当直线



(2)当直线



(3)当直线


由以上情况可知,数量积
考查方向
解题思路
1.先将题中给出的向量和所给的向量分类;
2.计算在不同类里数量积的不同值后即可得到答案。
易错点
1.不知如何分类导致结果多或者少;
2.无法理解题中的条件
知识点
14.某班主任在其工作手册中,对该班每个学生用十二项能力特征加以描述.每名学生的第
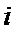
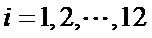
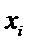
若学生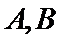
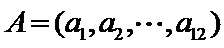
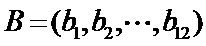
两名学生的不同能力特征项数为 (用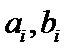
同学不同能力特征项数不少于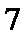
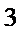
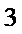
正确答案
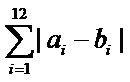
解析
设第三个学生为
因为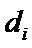
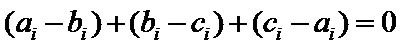
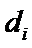
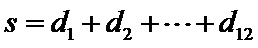
又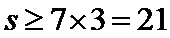
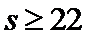
取
则不同能力特征项数总和恰为22 ,所以最小值为22 .
考查方向
解题思路
理解清题意即可得到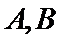
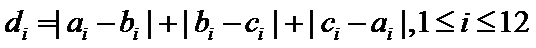
易错点
本题不易读懂题意,特别是对“
知识点
8.某大学的




正确答案
知识点
8.某大学的




正确答案
解析
分类讨论,有2种情形:
孪生姐妹乘坐甲车:则有
孪生姐妹不乘坐甲车:则有
所以共有24种,所以选A
考查方向
排列和组合的应用
解题思路
分类讨论,求出孪生姐妹乘坐甲车的情况,再求出孪生姐妹不乘坐甲车的情况
易错点
考虑情况不全面
知识点
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
甲乙两人进行围棋比赛,约定先连胜两局者直接赢得比赛,若赛完5局仍未出现连胜,则判定获胜局数多者赢得比赛,假设每局甲获胜的概率为,乙获胜的概率为,各局比赛结果相互独立。
(1)求甲在4局以内(含4局)赢得比赛的概率;
(2)记

正确答案
见解析。
解析
此题以古典概型和离散型随机变量分布列知识为背景,考察分析问题和解决问题的能力。
(1)p=
X可取值为2,3,4,5,其分布列为
∴E(X)=
知识点
(x+a)10的展开式中,x7的系数为15,则a=________。(用数字填写答案)
正确答案
解析
知识点
若
正确答案
解析
∵

∴8-r-
∴

知识点

正确答案
15
解析
二项展开式的通项为


知识点

正确答案
-160
解析
( 



知识点
已知函数
(1)当


(2)求函数
正确答案
(1) 


当



解析
函数


(1)当






即
(2)由
①当




②当








综上:当

当



知识点


正确答案
20
解析
通项



知识点
扫码查看完整答案与解析