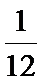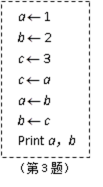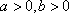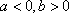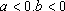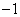- 计数原理
- 共551题
11.在

正确答案
45
解析
因为



考查方向
解题思路
(1)求二项展开式中的指定项,一般是利用通项公式进行化简通项公式后,令字母的指数符合要求(求常数项时,指数为零;求有理项时,指数为整数等),解出项数r+1,代回通项公式即可.(2)对于三项式问题一般先变形化为二项式再解决.
易错点
三项式与二项式之间的转化处理
知识点
9.在

正确答案
40
解析
利用通项公式,



考查方向
解题思路
写出二项式定理展开式的通项公式,利用x的指数为3,求出r,然后求解所求数值.
易错点
二项式通项公式正确运用
知识点
9.在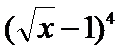
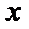
正确答案
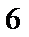
解析
由题可知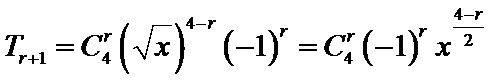
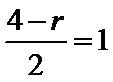
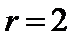
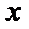
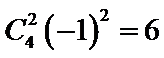
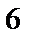
考查方向
解题思路
先列出通项公式,再根据x的次数解出r。
易错点
注意式子中的常数项为-1,在利用二项式定理时,要注意。
知识点
5.先后抛掷两枚均匀的正方体骰子(它们的六个面分别标有点数1、2、3、4、5、6),骰子朝上的面的点数分别为X、Y,则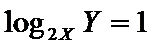
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.一个总体中有60个个体,随机编号0,1,2,…,59,依编号顺序平均分成6个小组,组号依次为1,2,3,…,6.现用系统抽样方法抽取一个容量为6的样本,若在第1组随机抽取的号码为3,则在第5组中抽取的号码是_______________
正确答案
43
解析
因为个体总数为60,组数为6,所以间隔是10,因此第5组抽取的号码为:3+10(5-1)=43.
考查方向
解题思路
由总体中的个体数及组数,就可求出间隔,
易错点
系统抽样是等距抽样,找不到等距的间隔。
知识点
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
在右图的算法中,最后输出的a,b的值依次是 .
正确答案
2,1
解析
第四步c变为1,第五步a变为2,第五步b变为1
知识点
12.在二项式
正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
8. 规定集合




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.

正确答案
1890
解析
解析已在路上飞奔,马上就到!
知识点









正确答案
解析
由
由正弦定理及

所以

故由

而




知识点
根据如下样本数据
得到的回归方程为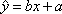
正确答案
解析
由题意可知:回归方程经过的样本数据对应的点附近,是减函数,所以b<0,且回归方程经过(3,4)与(4,3.5)附近,所以a>0。
知识点
若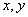
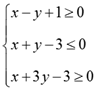

正确答案
解析
利用不等式组,作出可行域,可知区域表示的为三角形,当目标函数过点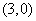

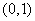
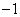
知识点
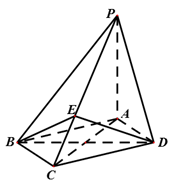
如图,四棱锥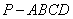
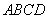
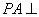
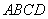
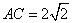
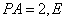
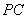
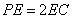
(1)证明: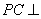
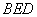
(2)设二面角

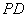
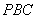
正确答案
见解析。
解析
设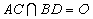
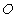
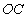
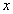
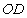
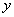
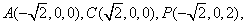
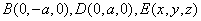
(1)证明:由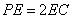

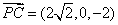
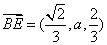
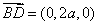

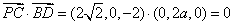
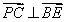
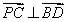
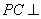
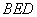
(2) 设平面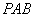
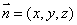
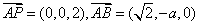

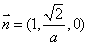
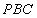
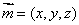
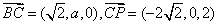
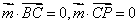
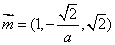
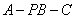
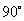

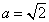
所以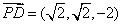
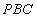
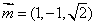
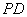
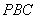

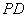
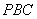
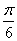
知识点
原命题为“若

正确答案
解析
知识点
扫码查看完整答案与解析