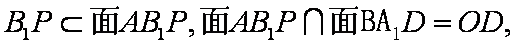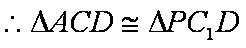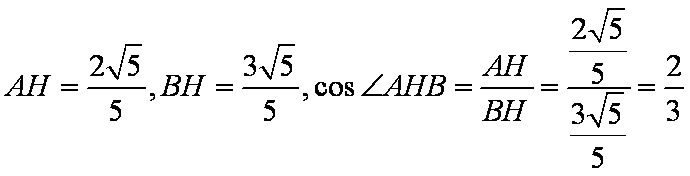平面向量_章节学习

1

题型：填空题

|

填空题 · 20 分

请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。

正确答案

测试

1

题型：填空题

|

填空题 · 20 分

请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。

正确答案

测试

1

题型：填空题

|

填空题 · 5 分

若的展开式中项的系数为20，则的最小值为。

正确答案

2

解析

将展开，得到，令.

由，得，所以.

知识点

单位向量

1

题型：填空题

|

填空题 · 5 分

已知向量与的夹角1200，且||=3，||=2，若，且，则实数的值为____________.

正确答案

解析

略。

知识点

单位向量

1

题型：简答题

|

简答题 · 12 分

正确答案

解析

知识点

单位向量

1

题型：简答题

|

简答题 · 10 分

在平面直角坐标系xOy中，求过椭圆 (φ为参数)的右焦点，且与直线(t为参数)平行的直线的普通方程。

正确答案

x-2y-4＝0

解析

由题设知，椭圆的长半轴长a＝5，短半轴长b＝3，从而c＝＝4，

所以右焦点为(4,0).将已知直线的参数方程化为普通方程：x-2y+2＝0.

故所求直线的斜率为，因此其方程为y＝(x-4)，即x-2y-4＝0.

知识点

单位向量

1

题型：单选题

|

单选题 · 5 分

已知和点M满足.若存在实数m使得成立，则m=

A2

B3

C4

D5

正确答案

B

解析

由题目条件可知，M为的重心，连接并延长交于，则 ①，因为为中线，

即 ②, 联立①②可得，故正确。

知识点

单位向量

1

题型：填空题

|

填空题 · 5 分

已知集合A＝{-1,1,2,4}，B＝{-1,0,2}，则A∩B＝________.

正确答案

{-1,2}

解析

由交集的定义知A∩B＝{-1,1,2,4}∩{-1,0,2}＝{-1,2}。

知识点

单位向量

1

题型：简答题

|

简答题 · 14 分

已知双曲线的左、右顶点分别为，点，是双曲线上不同的两个动点。

（1）求直线与交点的轨迹的方程；

（2）若过点的两条直线和与轨迹都只有一个交点，且，求的值。

正确答案

见解析。

解析

（1）解：由为双曲线的左右顶点知，

，，两式相乘，

因为点在双曲线上，所以，即，故，

所以，即直线与交点的轨迹的方程为.

（2）解法1：设，则由知，。

将代入得

，即，

由与E只有一个交点知，，即。

同理，由与E只有一个交点知，，消去得，即，

从而[来，又，。

解法2：由题意知直线和都是椭圆E的切线，由对称性知，两直线的倾斜角分别为和，设其方程为，代入椭圆E的方程得

，即

由得，即，

，

知识点

单位向量

1

题型：单选题

|

单选题 · 5 分

已知点A(1,3)，B(4，－1)，则与向量同方向的单位向量为(　　)。

A

B

C

D

正确答案

A

解析

与同方向的单位向量为＝，故选A

知识点

单位向量

1

题型：单选题

|

单选题 · 5 分

函数的一个零点落在下列哪个区;间（.）

A（0,1）

B（1,2）

C（2,3）

D（3,4）

正确答案

B

解析

根据函数的实根存在定理，要验证函数的零点的位置，只要求出函数在区间的两个端点上的函数值，得到结果。根据函数的实根存在定理得到f（1）•f（2）＜0.故选B

知识点

单位向量

1

题型：简答题

|

简答题 · 12 分

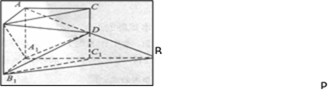
如图，在直三棱柱ABC-A1B1C1中，∠ BAC=90°，AB=AC=AA1 =1.D是棱CC1上的一点，P是AD的延长线与A1C1的延长线的交点，且PB1∥平面BDA1。

(1)求证：CD=C1D：

(2)求二面角A-A1D-B的平面角的余弦值；

(3)求点C到平面B1DP的距离。

正确答案

见解析

解析

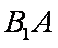
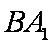
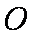
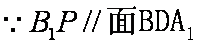
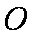
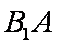
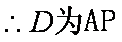
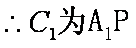
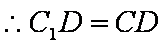
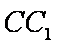
（1）连接交于,,

,又为的中点，

中点，,,D为的中点。

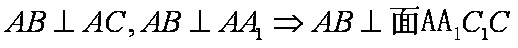
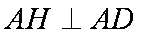
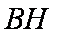
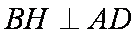
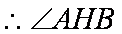
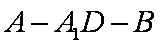
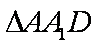
（2）由题意,过B 作,连接，则,为二面角的平面角。在中，,则

（3）因为，所以,

,

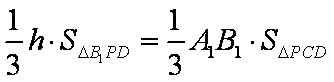
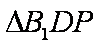
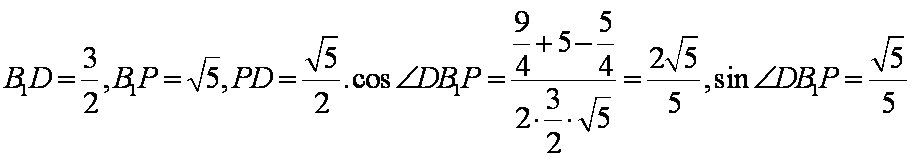
在中，，

知识点

单位向量

1

题型：简答题

|

简答题 · 13 分

已知椭圆:与双曲线有相同的焦点，且椭圆的离心率，又为椭圆的左右顶点，为椭圆上任一点（异于）。

（1）求椭圆的方程；

（2）若直线交直线于点，过作直线的垂线交轴于点，求的坐标；

（3）求点在直线上射影的轨迹方程。

正确答案

见解析。

解析

（1）由题意知,故椭圆方程为

（2）设，则由图知，得,故.

设,由得：，.

又在椭圆上，故，化简得，即

（3）点在直线上射影即PQ与MB的交点H，由得为直角三角形，设E为中点，则==，，因此H点的轨迹方程为

知识点

单位向量

1

题型：单选题

|

单选题 · 5 分

10. 设是单位向量，且，则的最小值为（）

A

B

C

D

正确答案

B

解析

解析已在路上飞奔，马上就到！

知识点

单位向量平面向量数量积的运算量积判断两个平面向量的垂直关系

1

题型：单选题

|

单选题 · 5 分

17．空间三点，则（）

A与是共线向量

B的单位向量是

C与夹角的余弦值

D平面的一个法向量是

正确答案

D

解析

解析已在路上飞奔，马上就到！

知识点

单位向量平行向量与共线向量数量积表示两个向量的夹角

热门试卷

正确答案

正确答案

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点