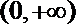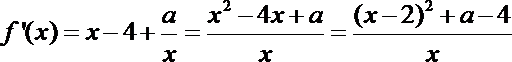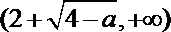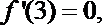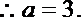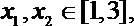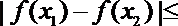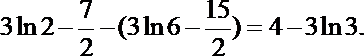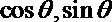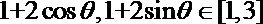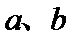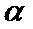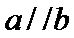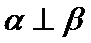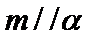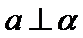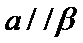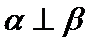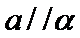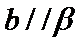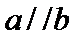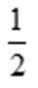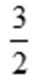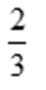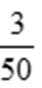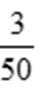- 平面向量
- 共1314题
21. 已知非零向量






(1)当

(2)设数列





正确答案
(1)


(2)∵ 
∴ 
∴ 

∴ 
∴ 

∴
解析
解析已在路上飞奔,马上就到!
知识点
6.已知:0<









正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知向量a=(
正确答案
解析
设选项中的向量与a的夹角为θ,对于选项A,由于cos θ=-



知识点
20.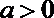
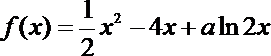
(1)求函数 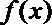
(2)当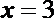
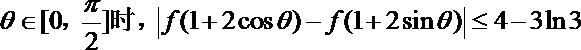
正确答案
(1)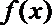
① 当
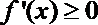
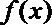
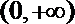
② 当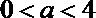
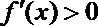
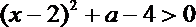
解得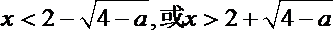
因此,函数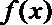
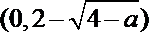
内也单调递增.
令
解得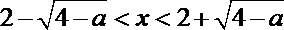
因此,函数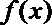
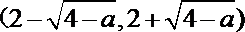
(2)当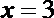
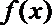

由(1)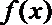
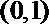
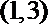
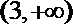
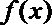
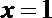
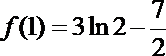
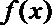
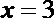

故在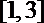
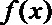
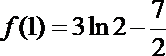

对于任意的
当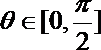
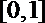
从而
解析
解析已在路上飞奔,马上就到!
知识点
4.设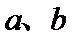
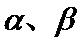
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3. 若


正确答案
解析
因为
考查方向
解题思路
根据向量平行时数量积的特点进行求解
易错点
混淆向量平行和向量垂直时,向量数量积不同。
知识点
16.在













正确答案
解析
因为
且

因为


考查方向
解题思路
根据给出的向量之间的关系和线段之间的关系,利用余弦定理求解
易错点
向量模和向量平行概念不理解
知识点
4. 已知P(B|A)= 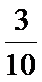
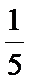
正确答案
解析
P(AB) = P(B|A) ·P(A)= 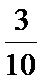
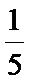
考查方向
解题思路
根据概率公式之间的转换公式计算
易错点
条件概率公式记混,不知道P(B|A)和P(A)的区别和联系
知识点
已知矩阵A的逆矩阵A﹣1=(
(1)求矩阵A;
(2)求矩阵A﹣1的特征值以及属于每个特征值的一个特征向量。
正确答案
(1)设A=


解得a=




(2)矩阵A﹣1的特征多项式为f(λ)=
令f(λ)=(λ﹣2)2﹣1=0,可求得特征值为λ1=1,λ2=3,
设λ1=1对应的一个特征向量为α=
则由λ1α=Mα,得x+y=0
得x=﹣y,可令x=1,则y=﹣1,
所以矩阵M的一个特征值λ1=1对应的一个特征向量为
同理可得矩阵M的一个特征值λ2=3对应的一个特征向量为
解析
计算题;矩阵和变换。
(1)利用AA﹣1=E,建立方程组,即可求矩阵A;
(2)先根据特征值的定义列出特征多项式,令f(λ)=0解方程可得特征值,再由特征值列出方程组即可解得相应的特征向量。
知识点
根据统计,一名工作组装第






正确答案
解析
由条件可知,


知识点
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
已知两个非零向量a,b满足|a+b|=
正确答案
解析
根据向量加法、减法的几何意义可知|a+b|与|a

知识点
已知向量





正确答案
解析
考查向量的夹角和向量的模长公式,以及向量三角形法则、余弦定理等知识,如图
知识点
若



正确答案
解析
∵
即


又∵

∴
而
=3﹣2
∴
故选B。
知识点
记


正确答案
解析
由向量运算的平行四边形法可知




(或
知识点
扫码查看完整答案与解析