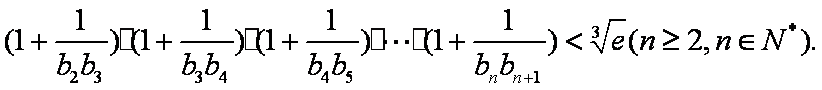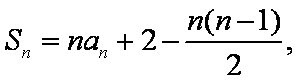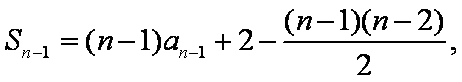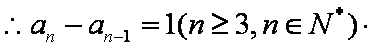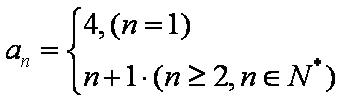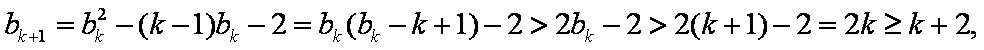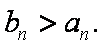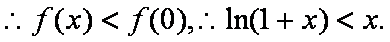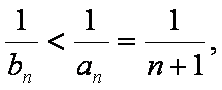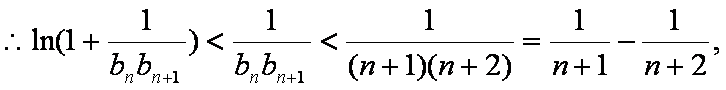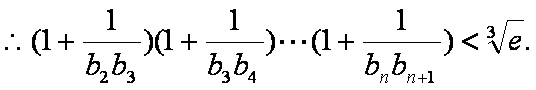- 直线、平面垂直的综合应用
- 共97题
三个城市襄阳、荆州、武汉分别位于









(1)设


(2)由(1)中建立的函数关系,确定货运中转站的位置,使修建的道路的总长度最短.
正确答案
见解析
解析
解析:(1)由题意可知


在

所以
又易知



(2)由(1)中建立的函数关系
因为




当







因此,当货运中转站建在三角形区内且到


知识点
设




①若



②若


③ 若



④ 若



其中错误命题的序号是( )
正确答案
解析
根据线面垂直的性质和判断可知,②③正确,错误的为①④,选A.
知识点
已知数列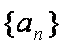
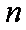
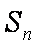
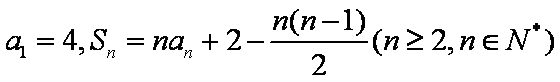
(1)求数列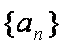
(2)设数列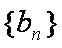
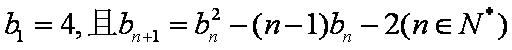

(3)求证:
正确答案
见解析。
解析
(1)当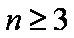
可得:
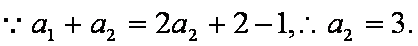
(2)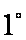
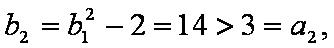


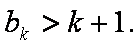
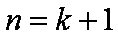
所以当n=k+l时,不等式也成立。
根据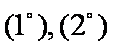
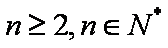
(3)设

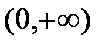

知识点
如图,已知长方形







(1)求证:
(2)若点



正确答案
见解析
解析
(1)因为平面AMD垂直ABCM,AB=2,AD=1,M时DC的中点,所以AD=DM,取AM的中点O,连结OD,则DO垂直平面ABCM,取AB得中点N,连结ON,则ON垂直AM,以O为原点如图建立空间直角坐标系,根据已知条件,得




(2)设


设平面

取


因为
求得


知识点
设


正确答案
解析


故


知识点
扫码查看完整答案与解析