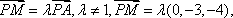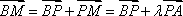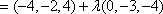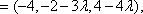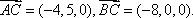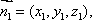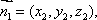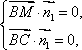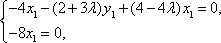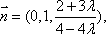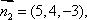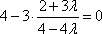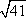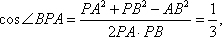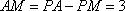- 直线、平面垂直的综合应用
- 共97题
函数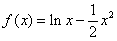
正确答案
解析
略。
知识点
如图,设

正确答案
解析
略
知识点
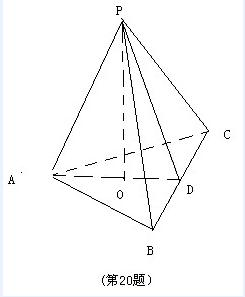
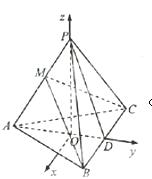
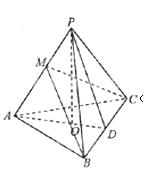
如图,在三棱锥P-ABC中,AB=AC,D为BC的中点,PO⊥平面ABC,垂足O落在线段AD上,已知BC=8,PO=4,AO=3,OD=2
(1)证明:AP⊥BC;
(2)在线段AP上是否存在点M,使得二面角A-MC-B为直二面角?若存在,求出AM的长;若不存在,请说明理由。
正确答案
见解析
解析
(1)证明:如图,以O为原点,以射线OP为z轴的正半轴,建立空间直角坐标系O-xyz
则O(0,0,0),A(0,-3,0),B(4,2,0),C(-4,2,0)
P(0,0,4)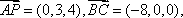
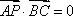
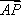

(2)解:设
设平面BMC的法向量
平面APC的法向量
由
得
即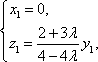
由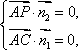
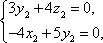
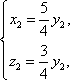
由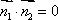
解得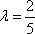
综上所述,存在点M符合题意,AM=3。
方法二:
(1)证明:由AB=AC,D是BC的中点,得AD⊥BC,
又PO⊥平面ABC,得PO⊥BC。
因为PO∩BC=0,所以BC⊥平面PAD
故BC⊥PA.
(2)解:如图,在平面PAD内作BM⊥PA于M,连CM.
由(Ⅰ)中知AP⊥BC,得AP⊥平面BMC.
又AP
在Rt⊿ADB中,AB2=AD2+BD2=41,得AB=
在Rt⊿POD中, PB2=PO2+OD2,
在Rt⊿PDB中, PB2=PD2+BD2,
所以PB2=PO2+OD2+BD2=36,得PB=6.
在Rt⊿POA中, PA2=AO2+OP2=25,得PA=5
又
从而
综上所述,存在点M符合题意,AM=3.
知识点
在

正确答案
解析
因为


即





知识点
4.下列命题正确的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析