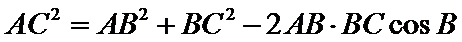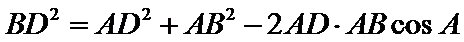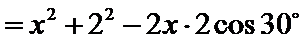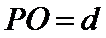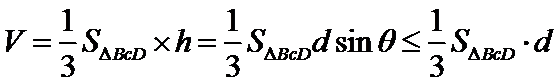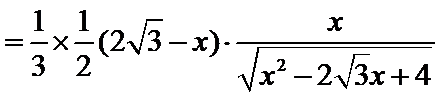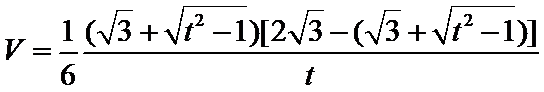- 直线、平面垂直的综合应用
- 共97题
14.如图,在
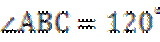
正确答案
解析
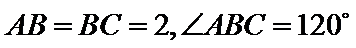
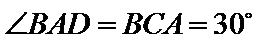
由余弦定理可得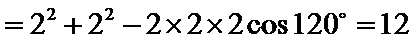
所以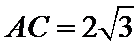
设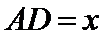
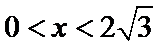
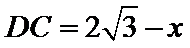
在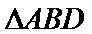
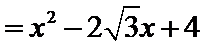
故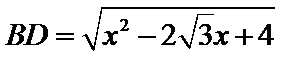
在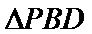
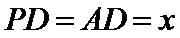
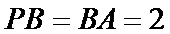
由余弦定理可得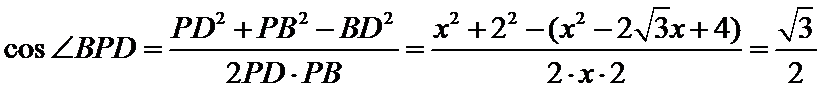
所以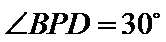
过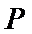
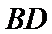
则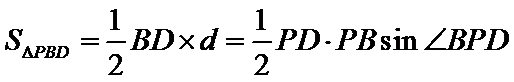
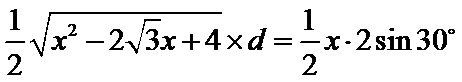
解得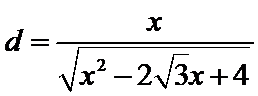
而
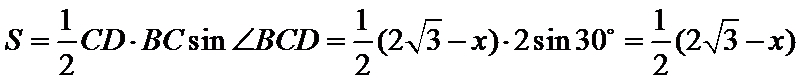
设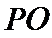
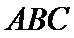
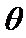
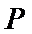
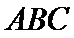
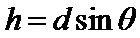
故四面体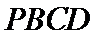
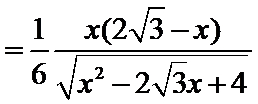
设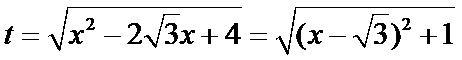
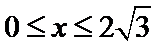
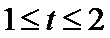
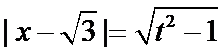
(2)当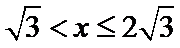
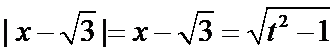
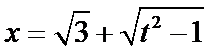
此时,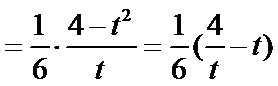
由(1)可知,函数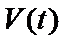
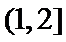
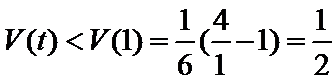
综上,四面体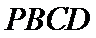
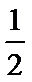
考查方向
解题思路
设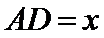
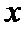
易错点
体积无法写成关于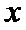
知识点
5.已知



正确答案
解析
由A选项,
















考查方向
解题思路
根据选项逐一进行判断
易错点
平面和直线的位置关系混淆,考虑问题不全面
知识点
如图,正方形ABCD的中心为O,四边形OBEF为矩形,平面OBEF⊥平面ABCD,点G为AB的中点,AB=BE=2.
(I)求证:EG∥平面ADF;
(II)求二面角O-EF-C的正弦值;
(III)设H为线段AF上的点,且AH=
正确答案
依题意,







(I)证明:依题意,










(II)解:易证,








因此有



(III)解:由









知识点
(本小题满分12分)
如图,在四棱锥P-ABCD中,AD∥BC,


(I)在平面PAB内找一点M,使得直线CM∥平面PBE,并说明理由;
(II)若二面角P-CD-A的大小为45°,求直线PA与平面PCE所成角的正弦值.
正确答案
(Ⅰ)在梯形ABCD中,AB与CD不平行.
延长AB,DC,相交于点M(M∈平面PAB),点M即为所求的一个点.理由如下:

所以四边形BCDE是平行四边形.
从而CM∥EB.
又EB

所以CM∥平面PBE.
(说明:延长AP至点N,使得AP=PN,则所找的点可以是直线MN上任意一点)
(Ⅱ)方法一:
由已知,CD⊥PA,CD⊥AD,PA
所以CD⊥平面PAD.
从而CD⊥PD.
所以
所以
设BC=1,则在Rt△PAD中,PA=AD=2.
过点A作AH⊥CE,交CE的延长线于点H,连接PH.
易知PA⊥平面ABCD,
从而PA⊥CE.
于是CE⊥平面PAH.
所以平面PCE⊥平面PAH.
过A作AQ⊥PH于Q,则AQ⊥平面PCE.
所以
在Rt△AEH中,
所以AH=
在Rt△PAH中,PH=

所以sin


知识点
7.若




正确答案
解析
若










考查方向
解题思路
利用直线与平面平行于垂直的关系,结合充分条件和必要条件性质,判断关系。
易错点
逻辑混乱,直线与平面的位置关系掌握不牢
知识点
如图,四边形ABCD为菱形,∠ABC=120°,E,F是平面ABCD同一侧的两点,BE⊥平面ABCD,DF⊥平面ABCD,BE=2DF,AE⊥EC.
19.证明:平面AEC⊥平面AFC;
20.求直线AE与直线CF所成角的余弦值.
正确答案
(Ⅰ)(Ⅰ)连接BD,设BD∩AC=G,连接EG,FG,EF,在菱形ABCD中,不妨设GB=1,由∠ABC=120°,可得AG=GC=
由BE⊥平面ABCD,AB=BC可知,AE=EC,
又∵AE⊥EC,∴EG=
在Rt△EBG中,可得BE=

在Rt△FDG中,可得FG=
在直角梯形BDFE中,由BD=2,BE=


∴
∵AC∩FG=G,∴EG⊥平面AFC,
∵EG
解析
见答案
考查方向
解题思路
(Ⅰ)连接BD,设BD∩AC=G,连接EG,FG,EF,在菱形ABCD中,不妨设GB=1易证EG⊥AC,通过计算可证EG⊥FG,根据线面垂直判定定理可知EG⊥平面AFC,由面面垂直判定定理知平面AFC⊥平面AEC;
易错点
本题在证明过程中推理不严密易错。
正确答案
(Ⅱ)
解析
(Ⅱ)如图,以G为坐标原点,分别以












故
所以直线AE与CF所成的角的余弦值为
考查方向
解题思路
(Ⅱ)以G为坐标原点,分别以


易错点
本题在写垂直的过程不能写全条件。
如图2,三角形












21.证明:
22.求二面角
23.求直线

正确答案
(1)见解析;
解析
(1)证明:∵ 


∴ 







∴ 



∴ 
考查方向
解题思路
第一问,利用面面垂直的性质定理,可得
易错点
定理的应用不熟练以及建系求角过程中,计算错误。
正确答案

解析
(2)∵ 
∴ 






∴ 




∴ 

∴ 

在



∴ 


考查方向
解题思路
第一问,利用面面垂直的性质定理,可得
易错点
定理的应用不熟练以及建系求角过程中,计算错误。
正确答案

解析
(3)如下图所示,连接
∵ 


∴ 
∴ 


在


由余弦定理可得
∴ 直线


考查方向
解题思路
第一问,利用面面垂直的性质定理,可得
易错点
定理的应用不熟练以及建系求角过程中,计算错误。
如图4,直三棱柱ABC-A



20.证明:平面AEF⊥平面B

21.若直线A



正确答案
如图,因为三棱柱
所以




所以
解析
见答案
考查方向
解题思路
先证明



易错点
不会证明

正确答案

解析
设AB的中点为D,连接









由题设知,
所以,
在


故三棱锥F-AEC的体积
考查方向
解题思路
设AB的中点为D,证明


由题设知,
易错点
找不到直线与平面所成的角;
如图4,直三棱柱ABC-A



20.证明:平面AEF⊥平面B

21.若直线A



正确答案
如图,因为三棱柱
所以




所以
解析
见答案
考查方向
解题思路
先证明



易错点
不会证明

正确答案

解析
设AB的中点为D,连接









由题设知,
所以,
在


故三棱锥F-AEC的体积
考查方向
解题思路
设AB的中点为D,证明


由题设知,
易错点
找不到直线与平面所成的角;
7.由棱锥和棱柱组成的几何体的三视图如图所示,则该几何体的体积为( )
正确答案
解析
由三视图可以看出该几何体是由三棱柱和三棱锥组成。所以几何体的体积为,
考查方向
解题思路
有三视图画出直观图根据直观图表示的几何体求体积。
易错点
在观察时候将底面的高看错。
知识点
扫码查看完整答案与解析