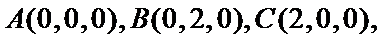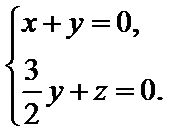- 直线、平面垂直的综合应用
- 共97题
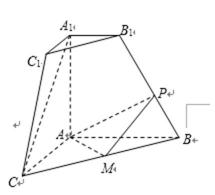
如图,五面体





18.求证:直线

19.求二面角
正确答案
略
解析
解:在直角梯形

可得:


又∵


又


可得:
由①②可得:直线

考查方向
解题思路
先证出




易错点
在证明面面垂直时,没有严格按照定理的条件论证,重点是线面垂直,易在过程的严密性上扣分。
正确答案
解析
在直角梯形

可得:


又∵


又


可得:
由①②可得:直线

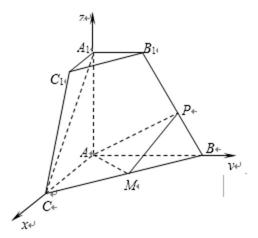
(Ⅱ)由(Ⅰ)知,建立如图空间直角坐标系,
由题意知各点坐标如下:

因此 
设平面

平面

由
可取
由
可取
于是
故二面角

考查方向
解题思路
(Ⅰ)先证出





易错点
(1).在证明面面垂直时,没有严格按照定理的条件论证,重点是线面垂直,易在过程的严密性上扣分。
(2).建立合理的坐标系,正确求点坐标
棱长为1的正方体





21.当


22.当平面



正确答案
(Ⅰ)略;
解析
(Ⅰ)连接


正方体









考查方向
线面、面面垂直的判定与性质,棱柱、棱锥体积的求法.
解题思路
证



易错点
通过证线面垂直得线线垂直;判断
正确答案

解析
当

取






















设



考查方向
解题思路
证



易错点
通过证线面垂直得线线垂直;判断
19. 如图,三棱柱ABC-A1B1C1所有的棱长均为2,B1在底面上的射影D在棱长BC上,且A1B∥平面ADC1。
(Ⅰ)求证:平面ADC1⊥平面BCC1B1;
(Ⅱ)求平面ADC1与平面A1AB所成角的正弦值.
正确答案
见解析
解析
(1)证明:
由题意得B1D⊥面ABC,直线ADㄈ面ABC,所以B1D⊥AD
连接A1C交AC1与点E,连接DE,则.
又因为A1B||ADC1
所以A1B||DE
在△A1BC中E是边A1C的中点,所以D为BC的中点
则AD⊥BC
又∵B1D∩BC=B
∴AD⊥平面BCC1B1
∵ADㄈ平面ADC1
∴平面ADC1⊥平面BCC1B1
(2)由(1)得以D为坐标原点,以DC,DA,DA1为xyz轴建系
因为
在平面A1AB中,不共线向量,
设法向量为
同理
在平面ADC1中,不共线向量,
设法向量为
由图知二面角α为锐角
考查方向
主要考察了直线与平面平行的判定与性质,考察了用空间向量求平面间的夹角
解题思路
第一步:根据已知条件A1B∥平面ADC1确定射影D的位置(底边中点)
第二步:根据线面垂直的判定得出:AD⊥平面BCC1B1进而得到面面垂直
第三步:根据第一问证明过程得出以D为坐标原点建系,利用空间向量求出结果
易错点
主要易错于点D位置的确定和面面角正弦值的求解
教师点评
该题思路比较简单,但是有几个关键地方必须考虑清楚:一个是D的位置判断,第二个就是求二面角的过程要细心,看好要求的结果
知识点
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠BCD=120°,四边形BFED为矩形,平面BFED⊥平面ABCD,BF=1.
21.求证:AD⊥平面BFED;
22.点P在线段EF上运动,设平面PAB与平面ADE所成锐二面角为θ,试求θ的最小值.
正确答案
见解析
解析
解:(1)在梯形
∵

∴
∴


平面

∴
∴

考查方向
解题思路
该题解题关键在于找到所求内容的突破点
1)根据余弦定理得出BD进而推出
2)由面面垂直得到线面垂直
3)设恰当的参数,建系求二面角,根据参数范围求θ的最小值
易错点
本题容易在
正确答案
见解析
解析
解:
(2)由(1)可建立分别以直线








∴
设

由
取
∵

∴
∵






∴
考查方向
解题思路
该题解题关键在于找到所求内容的突破点
1)根据余弦定理得出BD进而推出
2)由面面垂直得到线面垂直
3)设恰当的参数,建系求二面角,根据参数范围求θ的最小值
易错点
本题容易在
如图,在直三棱柱ABC-A1B1C1中,D1E分别为BB1和CC1的中点,AF⊥平面A1DE,其垂足F落在直线A1D上.
21.求证:BC⊥A1D;
22.若A1D=
正确答案
(1)BC⊥A1D;
解析
(1)∵在直三棱柱


又∵


又∵




又∵




而




∴

又∵


考查方向
解题思路
(1)通过证明线面垂直证线线垂直(2)利用空间直角坐标系,求出两个半平面的法向量再计算
易错点
忽视证明线线垂直的条件
正确答案
(2)
解析
(2)由(1)知







∵

则由


则






设平面

由



设平面

由



∴
∴二面角

考查方向
解题思路
(1)通过证明线面垂直证线线垂直(2)利用空间直角坐标系,求出两个半平面的法向量再计算
易错点
忽视证明线线垂直的条件
3.已知空间两条不同的直线


正确答案
解析
对于A:正确
对于B:正确应该是
对于C:
对于D:
考查方向
解题思路
本题属于常规题,可使用排除法解答,
易错点
该题易错于对判定定理不熟导致判断失误
知识点
如图,已知在直四棱柱(侧棱垂直底面的棱柱)



21.求证:

22.求

23.求二面角
正确答案
(1)略;
解析
以




则






又因为
所以,

考查方向
解题思路
建立空间直角坐标系,写出所需要的各个点的坐标,然后即可证明,
易错点
在建立坐标系时坐标写错;
正确答案
(2)
解析
(Ⅱ)设

由

得


又
设



即


考查方向
解题思路
先求平面
易错点
记错公式导致结果出错,主要是求正弦余弦弄不明白。
正确答案
(3)
解析
(Ⅲ)由(Ⅱ)知平面
设

由


得


设



所以二面角

考查方向
解题思路
分别求平面

易错点
无
已知四棱锥P-ABCD的三视图如下图所示,E是侧棱PC上的动点.
是否不论点E在何位置,都有BD⊥AE?证明你的结论;
若
正确答案
略(具体过程看解析);
解析
试题分析:本题属于立体几何中的基本问题,题目的难度是逐渐由易到难,由线面垂直去证明线线垂直; 不论点E在何位置,都有BD⊥AE.
证明如下:由三视图可知,四

∴BD⊥PC.又∵AC∩
都有AE⊂平面PAC.∴不论点E在何位置,都有BD⊥AE.
考查方向
解题思路
本题考查了证明线线垂直,空间向量在立体几何中的应用,解题步骤如下:根据题设应该由线面垂直去证明线线垂直。
易错点
对线线垂直转化为线面垂直的思路受阻;
正确答案
解析
试题分析:本题属于立体几何中的基本问题,题目的难度是逐渐由易到难,建好空间直角坐标系后,求出各点坐标,再求出法向量再算出夹角(亦可用传统法进行求解)。
解法1:在平面DAE内过点D作DF⊥AE于F,连结BF.
∵AD=AB=1,
∴Rt△ADE≌Rt△ABE,从而△AD
∴∠DFB为





解法2:如图,以点C为原点,CD,CB,CP所在的直线分别为x,y,z轴建立空间直角坐标系。则D(1,0,0),A(1,1,0),B(0,1,0),E(0,0,1),
从而



设平面ADE和平面ABE的法向量分别为

由
由


∴θ=


考查方向
解题思路
本题考查了证明线线垂直,空间向量在立体几何中的应用,解题步骤如下:建系,求出对应两个半平面的法向量,再由法向量的方面确定其夹角与二面角的关系。
易错点
二面角与法向量夹角之间是相等还是互补的判断。
如图,在直角梯形
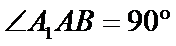
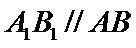
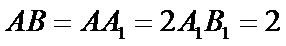
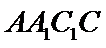
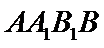
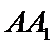
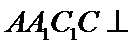

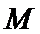

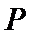
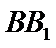
20.求证:
21.当点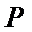
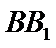
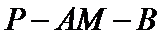
22.是否存在点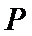
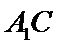
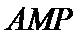
正确答案
见解析
解析
试题分析:本题属于立体几何中的基本问题,题目的难度是逐渐由易到难,(1)证明时要找到线线垂直关系得到线面才能下手去做;(2)要注意二面角与向量夹角之间的关系。
由已知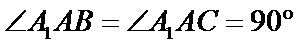
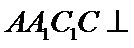

所以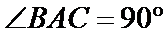
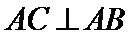
又因为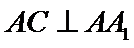
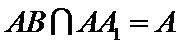
所以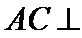
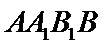
由已知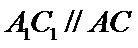
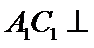
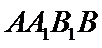
因为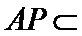
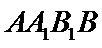
所以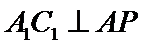
考查方向
解题思路
本题考查空间几何体的基本证明和二面角计算,解题步骤如下:
利用线面垂直这个思路得到线线垂直再结合已知证出结论。
建系计算出法向量再利用公式得出二、三问结论。
易错点
第二问判断二面角是锐角还是钝角时易出错。第三问在建系研究“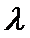
正确答案
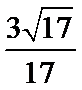
解析
试题分析:本题属于立体几何中的基本问题,题目的难度是逐渐由易到难,(1)证明时要找到线线垂直关系得到线面才能下手去做;(2)要注意二面角与向量夹角之间的关系。
(Ⅱ)由(Ⅰ)可知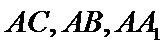
分别以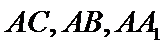
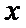

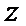
由已知 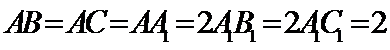
所以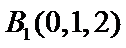
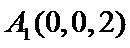
因为
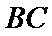
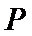

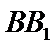
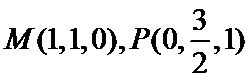
易知平面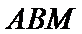

设平面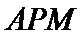
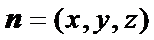
由 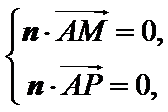
取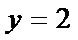
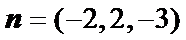
由图可知,二面角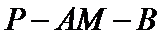
所以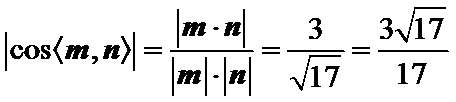
所以二面角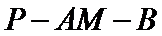
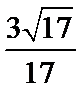
弦值;
考查方向
解题思路
本题考查空间几何体的基本证明和二面角计算,解题步骤如下:
利用线面垂直这个思路得到线线垂直再结合已知证出结论。
建系计算出法向量再利用公式得出二、三问结论。
易错点
第二问判断二面角是锐角还是钝角时易出错。第三问在建系研究“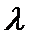
正确答案
在
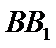
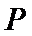
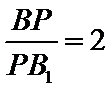
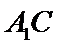
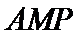
解析
试题分析:本题属于立体几何中的基本问题,题目的难度是逐渐由易到难,(1)证明时要找到线线垂直关系得到线面才能下手去做;(2)要注意二面角与向量夹角之间的关系。
存在点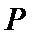
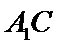
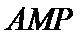
设

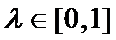

所以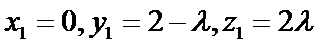
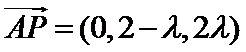
设平面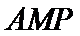
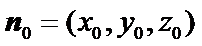
由 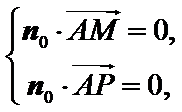
取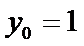
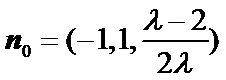
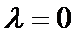
又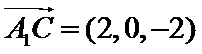
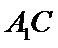
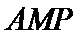
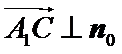
所以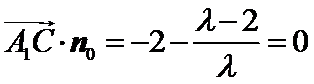
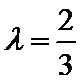
所以在

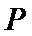
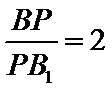

考查方向
解题思路
本题考查空间几何体的基本证明和二面角计算,解题步骤如下:
利用线面垂直这个思路得到线线垂直再结合已知证出结论。
建系计算出法向量再利用公式得出二、三问结论。
易错点
第二问判断二面角是锐角还是钝角时易出错。第三问在建系研究“
正方体





21.当


22.当平面



正确答案
(1)证明略;(2)
解析




正方体









考查方向
解题思路
利用线面垂直的判定定理及线面垂直的定义求证第1问
建立适当的空间直角坐标系,利用空间向量求解二面角的余弦值
易错点
平面的法向量计算出错
正确答案
(2)
解析
正方体



分别以





设







则



平面

平面







设平面


则
考查方向
解题思路
利用线面垂直的判定定理及线面垂直的定义求证第1问
建立适当的空间直角坐标系,利用空间向量求解二面角的余弦值
易错点
平面的法向量计算出错
扫码查看完整答案与解析