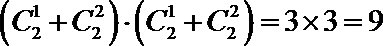- 函数的定义域及其求法
- 共125题
8.我们把平面内与直线垂直的非零向量称为直线的法向量.在平面直角坐标系中,利用求动点轨迹方程的方法,可以求出过点A(-3,4),且法向量为n=(1,-2)的直线方程为1×(x+3)+(-2)×(y-4)=0,即x-2y+11=0.类比上述方法,在空间直角坐标系中,经过点A(1,2,3),且法向量n=(-1,-2,1)的平面方程为______.
正确答案
x+2y-z-2=0
解析
类比直线方程的求法可得-1×(x-1)-2×(y-2)+1×(z-3)=0,即所求平面方程为x+2y-z-2=0.
知识点
3.已知函数f(x)的定义域为[3,6],则函数y=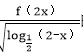
正确答案
解析
∵f(x)的定义域为[3,6],∴函数f(2x)中2x∈[3,6],∴
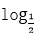

知识点
1.函数y=
正确答案
(-1,+∞)
解析
x+1>0,x>-1, (-1,+∞)
考查方向
解题思路
本题考查采用正确的方法求定义域的方法和不等式求解的能力,解题步骤如下:
分式有意义与二次根式有意义要求x+1>0,从而求出结果
易错点
本题必须注意分式有意义和二次根式有意义双重约束条件和定义域的区间表示,忽视则会出现错误。
知识点
11.已知函数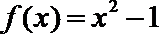
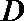
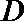
正确答案
9
解析
∵函数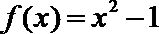
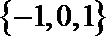
由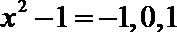
∴函数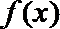
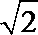
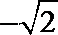
∴函数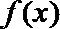
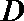
共9种可能,故这样的集合
考查方向
本题主要考查函数的概念及其构成元素、排列组合的知识,考查学生分析问题的能力,是容易题.
解题思路
由题意知,函数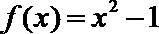
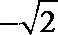
易错点
再求得定义域
知识点
15.已知函数


正确答案
解析
由题可知,x<-1时,f(x)>f(-1)=e,则g(x)的最大值为-1,则m∈
考查方向
解题思路
本题考查函数的图像性质,解题思路如下:画出函数f(x)的图像及g(x)的图像;比较函数值的大小,并求出最大值。
易错点
本题必须注意单调性的比较
知识点
扫码查看完整答案与解析