- 空间中直线与直线之间的位置关系
- 共26题
已知点







正确答案
解析
略
知识点
如图,在三棱柱ABC﹣A1B1C1中,侧棱AA1⊥底面ABC,AB⊥BC,D为AC的中点,AA1=AB=2。
(1)求证:AB1∥平面BC1D;
(2)若BC=3,求三棱锥D﹣BC1C的体积。
正确答案
见解析。
解析
(1)
证明:连接B1C,设B1C与BC1相交于O,连接OD,
∵四边形BCC1B1是平行四边形,∴点O为B1C的中点。
∵D为AC的中点,
∴OD为△AB1C的中位线,∴OD∥B1A。
OD⊂平BC1D,AB1⊄平面BC1D,
∴AB1∥平面BC1D。
(2)∵三棱柱ABC﹣A1B1C1,∴侧棱CC1∥AA1,
又∵AA1底面ABC,∴侧棱CC1⊥面ABC,
故CC1为三棱锥C1﹣BCD的高,A1A=CC1=2,
∴
∴
知识点
在空间,下列命题正确的是
正确答案
解析
由空间直线与平面的位置关系及线面垂直与平行的判定与性质定理可以很容易得出答案。
知识点
已知正方体的棱长为1,其俯视图是一个面积为1的正方形,侧视图是一个面积为
正确答案
解析
略。
知识点
如图,在正方体







正确答案
解析
略
知识点
在直三棱柱




(1)求证:
(2)若




正确答案
见解析。
解析
(1)
证明:



又






又 






又


(2)在直三棱柱







在



在
由(1)知





知识点
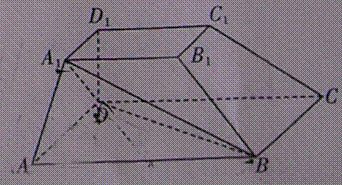
如图,在四棱台
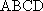
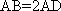
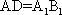
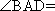
(1)证明: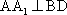
(2)证明: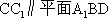
正确答案
见解析。
解析
(1)证明:因为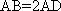
AD=a,则AB=2a,又因为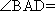
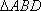
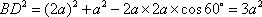
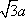

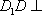
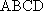


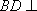
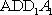
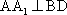
(2)连结AC,设AC
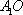
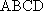
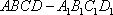
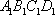
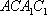
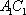
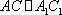
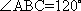
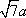
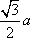
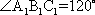
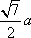
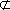


知识点
如图,弧
















(1)求异面直线

(2) 将

正确答案
(1)
解析
(1) 








(2)连结


由题设知,所得几何体为圆锥,其底面积为

该圆锥的体积为
知识点
已知









正确答案
解析
略
知识点
如图所示,在直三棱柱





(1)求证: 
(2)当面

(3)在(2)结论下,证明:

正确答案
见解析。
解析
证明:(1)设AB中点为G,连结GE,GC。

又EG∥
又
又因为MN//AB,所以
而
(2)因为面

面

面
所以
所以D为
(3)
因为EG//



所以


所以
又AB⊥CE,
所以

(3)方法二(略证):
过E点作

可用初中三角形相似或建立平面坐标系利用向量,直线斜率等方法证明
又
所以
所以
所以
又
所以
知识点
扫码查看完整答案与解析