- 抛物线及其性质
- 共507题
11.已知F1,F2是双曲线E: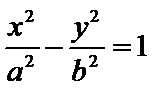


正确答案
知识点
设抛物线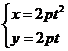
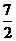
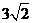
正确答案
知识点
22. 如图,在平面直角坐标系


⑴ 若直线


⑵ 已知抛物线



①求证:线段

②求
正确答案
(1)





⑵ ① 设点
则:

又

即
又




② 






知识点
20.已知抛物线的焦点为F,平行于x轴的两条直线分别交C于A,B两点,交C的准线于P,Q两点.
(I)若F在线段AB上,R是PQ的中点,证明AR∥FQ;
(II)若△PQF的面积是△ABF的面积的两倍,求AB中点的轨迹方程。
正确答案
见解析
解析
由题设



记过



(Ⅰ)由于


记




所以
(Ⅱ)设


则
由题设可得


设满足条件的

当



而

当




知识点
10.以抛物线C的顶点为圆心的圆交C于A、B两点,交C的标准线于D、E两点.已知|AB|=

正确答案
知识点
10.以抛物线C的顶点为圆心的圆交C于A、B两点,交C的标准线于D、E两点.已知|AB|=

正确答案
知识点
9.若抛物线
正确答案
9
知识点
若抛物线
正确答案
9
知识点
9.若抛物线
正确答案
9
解析
.
考查方向
解题思路
将到焦点的距离转化到准线的距离
易错点
没有转化到准线的距离
知识点
10.以抛物线C的顶点为圆心的圆交C于A、B两点,交C的准线于D、E两点.已知|AB|=

正确答案
解析
试题解析:如图,设抛物线方程为














考查方向
解题思路
先设出抛物线的标准方程,再根据勾股定理求出P,进而求出焦点到准线的距离.
易错点
解题时一定要注意运算的准确性与技巧性,基础题失分过多是相当一部分学生数学考不好的主要原因。
知识点
扫码查看完整答案与解析