抛物线及其性质
共507题

抛物线及其性质
共507题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 5 分

抛物线的焦点坐标为，则抛物线的方程为，若点在抛物线上运动，点在直线上运动，则的最小值等于（） .

正确答案

解析

略

知识点

抛物线的定义及应用

题型：简答题

简答题 · 14 分

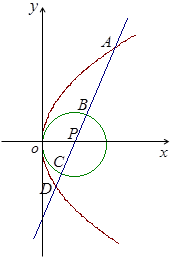
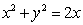
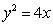
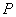
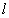
给定圆P:及抛物线S:,过圆心作直线,此直线与上述两曲线

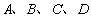
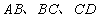
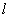
的四个交点,自上而下顺次记为,如果线段的长按此顺序构成一个等差数列,求直线的方程。

正确答案

见解析。

解析

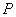
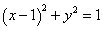
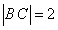
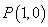
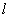
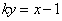
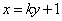
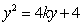
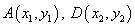
圆的方程为,则其直径长,圆心为,设的方程为,即,代入抛物线方程得:,设，

有,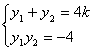

则.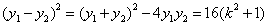

故

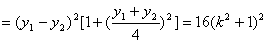
因此.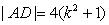

据等差,,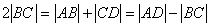

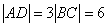
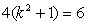
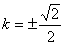
所以，即,，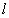

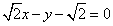
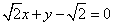
即：方程为或.

知识点

抛物线的定义及应用

题型：单选题

单选题 · 5 分

设抛物线的焦点为F，过F作直线交抛物线于A、B两点，若线段AB的中点E到y轴的距离为3，则弦AB的长为（）

C10

D12

正确答案

解析

如图，选C.

知识点

抛物线的定义及应用

题型：单选题

单选题 · 5 分

过抛物线焦点的直线交抛物线于，两点，若，则的中点到轴的距离等于（）

正确答案

解析

略

知识点

抛物线的定义及应用

题型：填空题

填空题 · 5 分

已知是曲线的焦点，，则的值是。

正确答案

解析

略

知识点

抛物线的定义及应用参数方程化成普通方程抛物线的参数方程

题型：单选题

单选题 · 5 分

设抛物线的顶点在原点,准线方程为则抛物线的方程是( )

正确答案

解析

∵准线方程为x=-2

∴=2

∴p=4

∴抛物线的方程为y2=8x

故选B

知识点

抛物线的定义及应用

题型：填空题

填空题 · 4 分

平面直角坐标系中，方程的曲线围成的封闭图形绕轴旋转一周所形成的几何体的体积为。

正确答案

解析

略

知识点

抛物线的定义及应用

题型：填空题

填空题 · 5 分

曲线是平面内到定点的距离与到定直线的距离之和为3的动点的轨迹. 则曲线与轴交点的坐标是（）；又已知点（为常数），那么的最小值=（） .

正确答案

解析

略

知识点

抛物线的定义及应用抛物线的标准方程和几何性质定义法求轨迹方程

题型：简答题

简答题 · 14 分

已知抛物线：，为直线上任意一点，过点作抛物线的两条切线，切点分别为,.

（1）当的坐标为时，求过三点的圆的方程；

（2）证明：以为直径的圆恒过点.

正确答案

见解析

解析

（1）解：当的坐标为时，设过点的切线方程为，

由消得. 1

令，解得.

代入方程1，解得.

设圆心的坐标为，由，得，解得.

故过三点的圆的方程为。

（2）证明：设，由已知得，，设切点分别为，，

所以，，

切线的方程为即，

切线的方程为即。

又因为切线过点，所以得. ①

又因为切线也过点，所以得. ②

所以，是方程的两实根，

由韦达定理得。

因为，，

所以

。

将代入，得.

所以以为直径的圆恒过点。

知识点

抛物线的定义及应用

题型：填空题

填空题 · 5 分

抛物线的准线方程为；经过此抛物线的焦点是和点，且与准线相切的圆共有个。

正确答案

， 2

解析

略

知识点

抛物线的定义及应用

继续学习学习下一知识点

下一知识点 : 直线与圆锥曲线的位置关系

百度题库 > 高考 > 理科数学 > 抛物线及其性质

扫码查看完整答案与解析