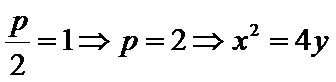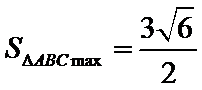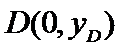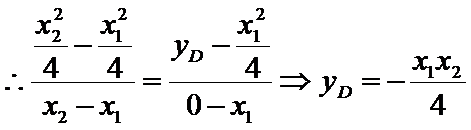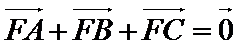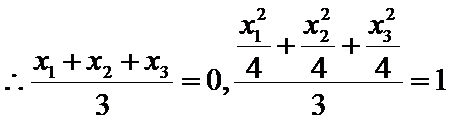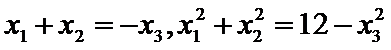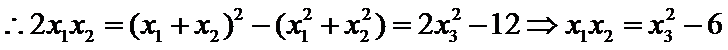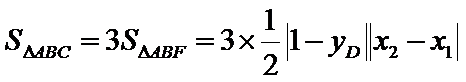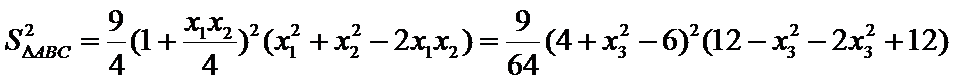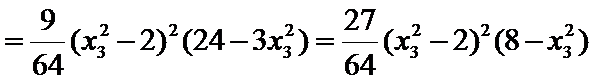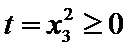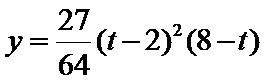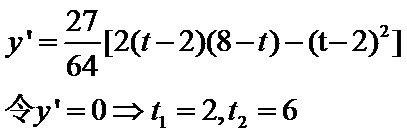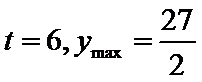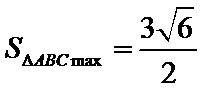- 抛物线及其性质
- 共507题
16.下列极坐标方程中,对应的曲线为右图的是( )
正确答案
知识点
设O为坐标原点,P是以F为焦点的抛物线


正确答案
知识点
如图,在平面直角坐标系


34.若直线


35.已知抛物线



①求证:线段

②求
正确答案

解析



即抛物线的焦点为

考查方向
解题思路
易错点
抛物线方程的形式,设而不求的思想。直线与抛物线的位置关系的运算程序。
正确答案
① 设点
则:

又

即
又




解析
① 设点
则:

又

即
又




② 






考查方向
解题思路
易错点
抛物线方程的形式,设而不求的思想。直线与抛物线的位置关系的运算程序。
9.若抛物线
正确答案
9
解析
.
考查方向
解题思路
将到焦点的距离转化到准线的距离
易错点
没有转化到准线的距离
知识点
设抛物线C:y2=2px(p>0)的焦点为F,点T(t,0)(t>0),且过点F的直线,交C于A,B.
22.当t=2时,若过T的直线交抛物线C于两点,且两交点的纵坐标乘积为-4,求焦点F的坐标;
23.如图,直线AT、 BT分别交抛物线C于点P、Q,连接PQ交x轴于点M,证明:|OF|,|OT|,|OM|成等比数列。
正确答案
见解析
解析
考查方向
解题思路
直线方程和抛物线方程方程联立,运用韦达定理,待定P的值,再利用几何性质解决实际问题。
易错点
解析几何最大的错误源于计算,所以容易出现计算错误。
正确答案
见解析
解析
考查方向
解题思路
直线方程和抛物线方程方程联立,运用韦达定理,待定P的值,再利用几何性质解决实际问题。
易错点
解析几何最大的错误源于计算,所以容易出现计算错误。
已知点F(0,1)为抛物线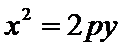
24.求抛物线C的方程;
25.点A、B、C是抛物线上三点且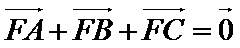
正确答案
(1)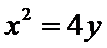
解析
(1)由题意知
考查方向
解题思路
1)第一问利用抛物线的定义,可求出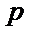
2)第二问首先设出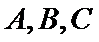
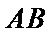
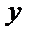
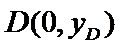
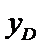
易错点
错位相减法求和计算容易错。
正确答案
(2)
解析
(2)令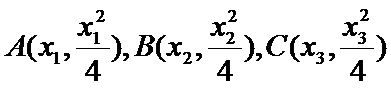
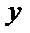
又因为
从而
令
当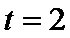
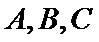
当
考查方向
解题思路
1)第一问利用抛物线的定义,可求出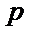
2)第二问首先设出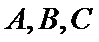
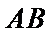
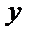
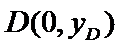
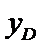
易错点
错位相减法求和计算容易错。
20. 已知F(







(Ⅰ)求抛物线方程和N点坐标;
(Ⅱ)判断直线




正确答案
见解析
考查方向
抛物线的性质与特征,圆锥曲线中的最值问题
解题思路
建立适当的坐标系,利用直线斜率之间的关系建立方程,进而求解,与抛物线联立成方程组,整理可得。
易错点
计算能力弱,找不到面积最小时候的情况
知识点
扫码查看完整答案与解析