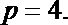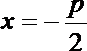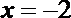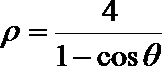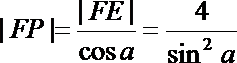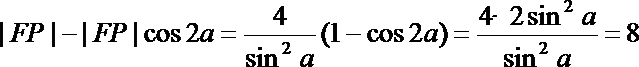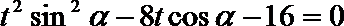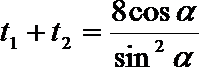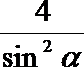抛物线及其性质
共507题

抛物线及其性质
共507题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 4 分

7．已知为抛物线上一点，设到准线的距离为，到点的距离为，则的最小值为________．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

抛物线的定义及应用

题型：填空题

填空题 · 5 分

15．已知点Ｆ为抛物线的焦点，O为原点，点Ｐ是抛物线准线上一动点，Ａ在抛物线上，且=4，则＋的最小值是__________。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

抛物线的定义及应用

题型：单选题

单选题 · 5 分

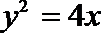
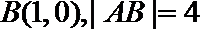
6．已知点A是抛物线上的点，点，则点A的横坐标为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

抛物线的定义及应用

题型：填空题

填空题 · 4 分

4．抛物线的准线方程是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

抛物线的定义及应用抛物线的标准方程和几何性质

题型：简答题

简答题 · 12 分

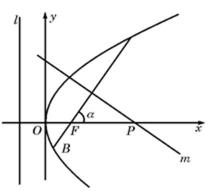
22．如图，倾斜角为α的直线经过抛物线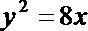的焦点F，且与抛物线交于A、B两点。

（1）求抛物线的焦点F的坐标及准线l的方程；

（2）若α为锐角，作线段AB的垂直平分线m交x轴于点P，证明|FP|-|FP|cos2α为定值，并求此定值

正确答案

（1）

解：设抛物线的标准方程为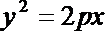，则，从而

因此焦点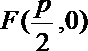的坐标为（2，0）.

又准线方程的一般式为

从而所求准线l的方程为

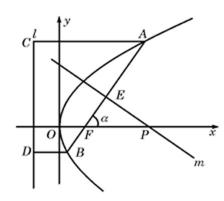
（2）解法一：如图（21）图作AC⊥l，BD⊥l，垂足为C、D，以F点为极点，F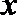为极轴建立极坐标系

则由抛物线的定义知抛物线方程为

则，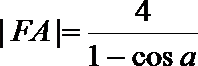

。

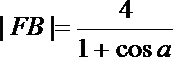
记直线m与AB的交点为E，则

所以

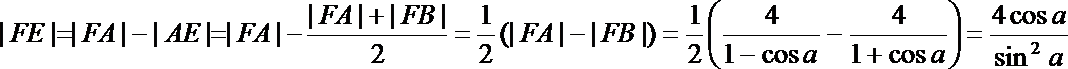
故

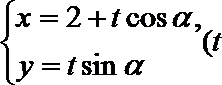
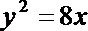
解法二：设直线AB：为参数）代入,得

因为直线AB与抛物线有两个交点，因此上述方程有两个根，设两个根分别为 t1，t2，

则

所以|FE|=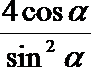, |FP|=

从而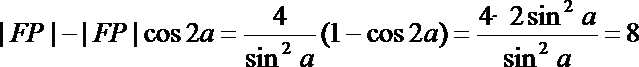为定值。

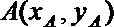
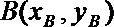
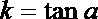
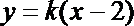
解法三：设，，直线AB的斜率为，则直线方程为。

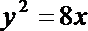
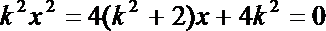
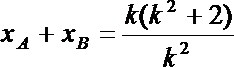
将此式代入,得，故。

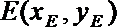
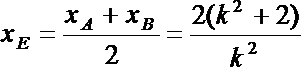
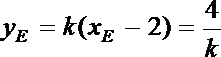
记直线m与AB的交点为，则

，

故直线m的方程为.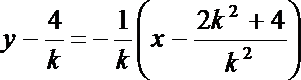

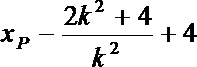
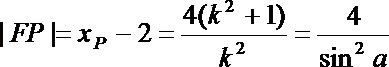
令y=0,得P的横坐标故

。

从而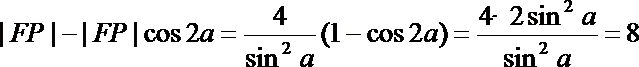为定值。

解析

解析已在路上飞奔，马上就到！

知识点

抛物线的定义及应用

题型：简答题

简答题 · 16 分

22．已知抛物线。

（1）的三个顶点在抛物线上，记的三边所在直线的斜率分别为，若点在坐标原点，求的值；

（2）请你给出一个以为顶点，且其余各顶点均为抛物线上的动点的多边形，写出多边形各边所在直线的斜率之间的关系式，并说明理由。

正确答案

（1）设，．则

．

（2） ① 研究．

．

② 研究四边形．

．

③ 研究五边形．

．

④ 研究边形，其中．

．

⑤ 研究边形，其中．

．

⑥研究边形，其中．

．

解析

解析已在路上飞奔，马上就到！

知识点

抛物线的定义及应用

题型：单选题

单选题 · 5 分

6. 若动圆的圆心在抛物线上，且与直线相切，则此圆恒过定点（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

抛物线的定义及应用

题型：简答题

简答题 · 13 分

20．如图，是抛物线为上的一点，弦SC，SD分别交x轴于A，B两点，且SA=SB。

（1）求证：直线CD的斜率为定值；

（2）延长DC交x轴于点E，若，求的值。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

抛物线的定义及应用

题型：填空题

填空题 · 5 分

14.过的直线交抛物线于、两点，则________。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

抛物线的定义及应用

题型：简答题

简答题 · 12 分

21.已知抛物线在x轴的正半轴上，过M的直线与C相交于A、B两点，O为坐标原点。

（I）若m=1，且直线的斜率为1，求以AB为直径的圆的方程；

（II）问是否存在定点M，不论直线绕点M如何转动，使得恒为定值。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

抛物线的定义及应用

继续学习学习下一知识点

下一知识点 : 直线与圆锥曲线的位置关系

百度题库 > 高考 > 理科数学 > 抛物线及其性质

扫码查看完整答案与解析