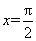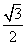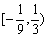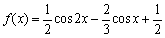- 正弦函数的奇偶性
- 共48题
已知函数
(1)求
(2)若


正确答案
见解析。
解析
(1)
(2)
因为

所以
知识点
已知函数f(x)=cos xsin 2x,下列结论中错误的是( )。
正确答案
解析
由题意知f(x)=2cos2x·sin x=2(1-sin2x)sin x.
令t=sin x,t∈[-1,1],
则g(t)=2(1-t2)t=2t-2t3.
令g′(t)=2-6t2=0,得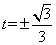
当t=±1时,函数值为0;
当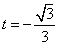
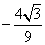
当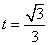
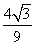
∴g(t)max=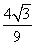
即f(x)的最大值为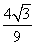
知识点
在平面直角坐标系






(1)求动点

(2)设过点








正确答案
(1)
(2)
解析
(1)解:设动点


整理得
所以动点


(2)当直线


当直线


将



设



设



所以
由题意可知
又直线

令

当


当


综上所述,点

知识点
已知函数f(x)=|x﹣2|﹣|x﹣5
(1)证明:﹣3≤f(x)≤3;
(2)求不等式f(x)≥x2﹣8x+15的解集。
正确答案
见解析
解析
(1)f(x)=|x﹣2|﹣|x﹣5|=
当2<x<5时,﹣3≤2x﹣7≤3
所以,﹣3≤f(x)≤3
(2)由(Ⅰ)可知
当x≤2时,f(x)≥x2﹣8x+15的解集为空集;
当2<x<5时,f(x)≥x2﹣8x+15的解集为{x|5﹣
当x≥5时,f(x)≥x2﹣8x+15的解集为{x|5≤x≤6}
知识点
在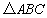
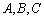
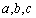
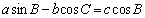
(1)判断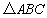
(2)若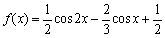
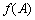
正确答案
(1)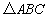
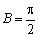
(2)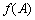
解析
(1)解:(法1)因为 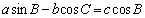
由正弦定理可得 
即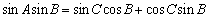
所以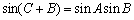
因为在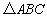
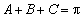
所以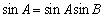
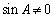
所以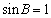
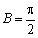
所以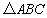
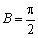
(法2)因为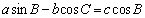
由余弦定理可得 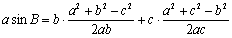
即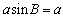
因为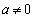
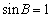
所以在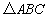
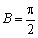
所以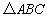
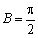
(2)解:因为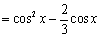
=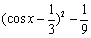
所以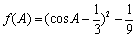
因为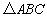
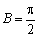
所以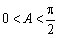
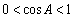
所以当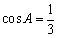
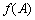
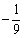
所以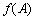
知识点
扫码查看完整答案与解析