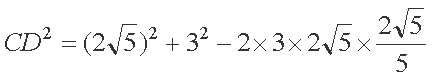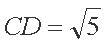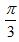- 正弦函数的奇偶性
- 共48题
已知






(1)求
(2)当


正确答案
(1)
解析
(1)因为
即

所以 
(2)由
故
由


由正弦定理,

故
知识点
在△ABC中,已知A=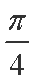

(1)求cosC的值;
(2)若BC=2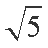
正确答案
见解析。
解析
(1)
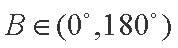
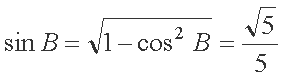
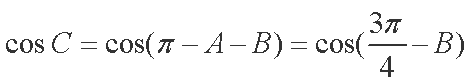
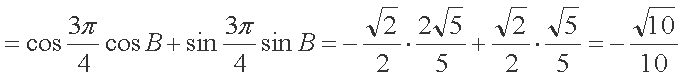
(2)由(1)可得
由正弦定理得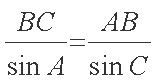
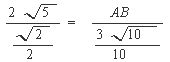
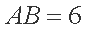
在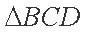

知识点

正确答案
解析



知识点
四棱锥










(1)求证:
(2)若

的余弦值;
(3)若



正确答案
见解析
解析
(1)证明:取


因为
所以
因为菱形

所以
所以
因为
所以

所以
(2)解:由(1)知
因为侧面

且平面

所以

以

则



因为


所以 

所以平面

因为 

设平面

令




由图可知,二面角

(3)解:因为

由(2)知

若设

由

在平面


所以平面

又因为

所以
即

所以,当


知识点
在△
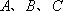
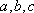
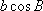
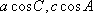
正确答案
解析
略
知识点
扫码查看完整答案与解析