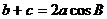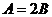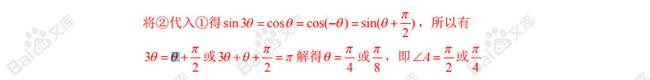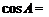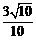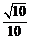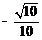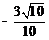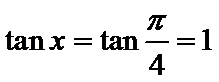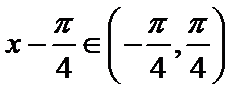- 正弦函数的奇偶性
- 共48题
13. 设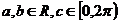
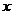
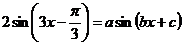
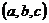
正确答案
4
解析
知识点
请考生从2题中选做一题
14.(坐标系与参数方程选做题)已知直线





15.(几何证明选讲选作题)如图1,已知












正确答案

解析
依题已知直线








考查方向
解题思路
先将直线
易错点
极坐标与平面直角坐标的互化。
正确答案

解析
如下图所示,连接












考查方向
解题思路
连接OC,则易得

易错点
图形中几何关系的寻找,射影定理的应用。
16.在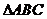
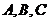
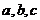
(Ⅰ)证明:
(Ⅱ)若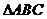
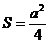
正确答案
知识点
8.在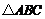
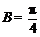
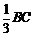
正确答案
知识点
6.某三棱锥的三视图如图所示,则该三棱锥的体积为()
正确答案
解析
分析三视图可知,该几何体为一三棱锥

考查方向
解题思路
解决此类问题的关键是根据几何体的三视图判断几何体的结构特征:主左同高,左俯同宽,主俯同长
易错点
1)几何体的三视图判断几何体的结构特征,2)求几何体的体积公式
知识点
8.





结论正确的是( )
正确答案
解析
如图,
由题意,












考查方向
解题思路
先根据向量相关性质把有向线段用坐标的形式表示出来,然后利用垂直关系求得。
易错点
计算错误,向量的数量积表示错误
知识点
在平面直角坐标系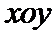
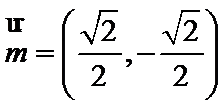
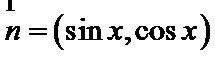
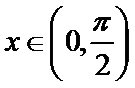
16.若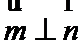
17.(2)若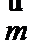
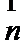
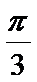
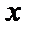
正确答案
(1)
解析
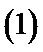
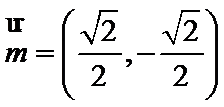
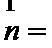
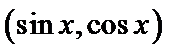
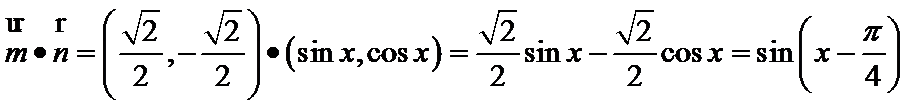


考查方向
解题思路
第一问,由两向量垂直,利用数量积等于零,结合坐标运算,可以得出正切值。
易错点
求解过程中注意角的范围,避免出现错解、多解现象
正确答案
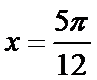
解析
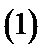
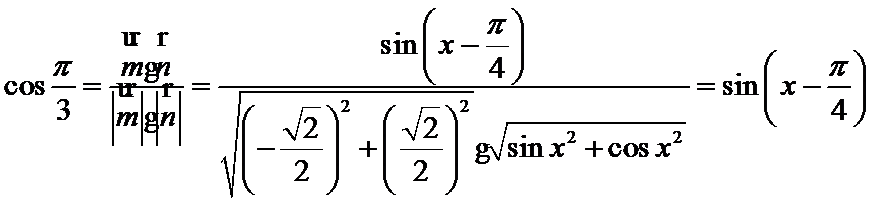

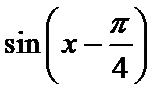
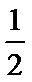

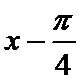
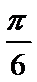

考查方向
解题思路
第二问,结合向量的夹角公式,列出方程求解即可。
易错点
求解过程中注意角的范围,避免出现错解、多解现象
已知





正确答案
解析
由







考查方向
本题主要考查了矩阵的概念,三角函数图像与性质的综合应用
易错点
函数平移的对象是x,这是解决函数平移的问题的关键
知识点
扫码查看完整答案与解析