双曲线的定义及标准方程
共193题

· 双曲线的定义及标准方程

双曲线的定义及标准方程
共193题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

9. 如图，直线与双曲线的左右两支分别交于、两点，与双曲线的右准线相交于点，为右焦点，若，又，则实数的值为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

双曲线的定义及标准方程

题型：填空题

填空题 · 5 分

16.已知函数f(x)=sin x- + .当<x<1时，不等式f(x)·log2(x-2m+)>0恒成立，则实数m的取值范围是_______.

正确答案

m≤- 2

解析

∵f'(x)=cos x-，当<x<1时，f'(x)>0,

即函数f(x)在(,1)上单调递增，此时f(x)>f()=sin>0,

又不等式f(x)·log2(x-2m+)>0恒成立,

∴log2(x-2m+)>0，即x-2m+>1恒成立,则x>2m+恒成立,

∵<x<1,

∴2m+≤⇒m≤-2.

知识点

双曲线的定义及标准方程

题型：填空题

填空题 · 5 分

6．若椭圆的左、右焦点分别为，线段被抛物线的焦点分成5﹕3的两段，则此椭圆的离心率为___________。

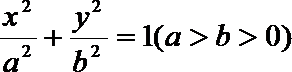
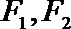
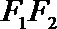
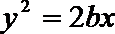
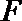
正确答案

解析

解析已在路上飞奔，马上就到！

知识点

双曲线的定义及标准方程

题型：填空题

填空题 · 5 分

12．已知x，y的值如下表所示：

如果y与x呈线性相关且回归直线方程为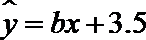，那么b=________________。

正确答案

0.5

解析

解析已在路上飞奔，马上就到！

知识点

双曲线的定义及标准方程

题型：单选题

单选题 · 5 分

8.若双曲线(a，b>0)的离心率e=2，右焦点为F(c，0)，方程ax2+2bx+c=0的两个实根分别是x1和x2，则点P(x1，x2)到原点的距离为（）

正确答案

解析

因为e==2，所以c=2a，所以b2=c2-a2=3a2，即b=.

因为x1+x2=-=-，x1x2==2，

所以点P(x1，x2)到原点(0，0)的距离d==.

知识点

双曲线的定义及标准方程双曲线的相关应用

题型：填空题

填空题 · 5 分

13.如果圆锥曲线=1的焦距与实数λ无关，那么它的焦点坐标是。

正确答案

解析

若=1为双曲线，则有(λ+5)(2－λ)>0

即－5<λ<2，这时a2=λ+5，b2=2－λ

于是c==.

显然焦点在y轴上，得此时的焦点坐标为(0，±)

若=1为椭圆，则有⇒λ>2

这时a2=λ+5，b2=λ－2，于是c==.

显然焦点在y轴上，得此时的焦点坐标为(0，±).

知识点

双曲线的定义及标准方程

题型：填空题

填空题 · 5 分

7.以抛物线y2=4x的焦点为顶点，顶点为中心，离心率为2的双曲线方程是_______。

正确答案

解析

抛物线的焦点为(1，0)，

则双曲线中a=1，且e==2，得c=2，

又c2=a2+b2，得b3=3，

则双曲线的方程为.

知识点

双曲线的定义及标准方程抛物线的标准方程和几何性质

题型：填空题

填空题 · 5 分

13.如果圆锥曲线=1的焦距与实数λ无关，那么它的焦点坐标是。

正确答案

解析

若=1为双曲线，则有(λ+5)(2－λ)>0

即－5<λ<2，这时a2=λ+5，b2=2－λ

于是c==.

显然焦点在y轴上，得此时的焦点坐标为(0，±).

若=1为椭圆，则有⇒λ>2.

这时a2=λ+5，b2=λ－2，于是c==.

显然焦点在y轴上，得此时的焦点坐标为(0，±).

知识点

双曲线的定义及标准方程

题型：单选题

单选题 · 5 分

6.到两条互相垂直的异面直线的距离相等的点，在过其中一条直线且平行于另一条直线的平面内的轨迹是（）

A直线

B椭圆

C抛物线

D双曲线

正确答案

解析

在边长为a的正方体ABCD-A1B1C1D1中，DC与A1D1是两条互相垂直的异面直线

平面ABCD过直线DC且平行于A1D1，以D为原点

分别以DA，DC所在直线为x轴，y轴建立平面直角坐标系

设点P(x，y)在平面ABCD内，且到A1D1与DC的距离相等

则|x|=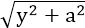，整理得x2-y2=a2.

知识点

双曲线的定义及标准方程直接法求轨迹方程

题型：填空题

填空题 · 4 分

7．设是实数．若方程表示的曲线是双曲线，则的取值范围为__________．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

双曲线的定义及标准方程

继续学习学习下一知识点

下一知识点 : 双曲线的几何性质

百度题库 > 高考 > 文科数学 > 双曲线的定义及标准方程

扫码查看完整答案与解析