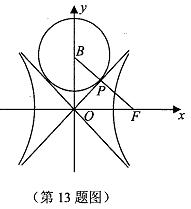
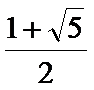双曲线的定义及标准方程
共193题

· 双曲线的定义及标准方程

双曲线的定义及标准方程
共193题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 14 分

本题共有2个小题，第1小题满分6分，第2小题满分8分.

双曲线的左、右焦点分别为F1、F2，直线l过F2且与双曲线交于A、B两点.

23.若l的倾斜角为，是等边三角形，求双曲线的渐近线方程；

24.设若l的斜率存在，且|AB|=4，求l的斜率.

第(1)小题正确答案及相关解析

正确答案

双曲线的渐近线方程为

解析

解：设．

由题意，，，，

因为是等边三角形，所以，

即，解得．

故双曲线的渐近线方程为．

考查方向

直线与圆锥曲线的位置关系

解题思路

利用等边三角形的性质和双曲线中，得到参数的关系，求出参数

易错点

弦长的运算

第(2)小题正确答案及相关解析

正确答案

斜率为．

解析

解：

由已知，．

设，，直线．

由，得．

因为与双曲线交于两点，所以，且．

由，，得，

故，

解得，故的斜率为．

考查方向

直线与圆锥曲线的位置关系

解题思路

联立方程组，根据弦长公式求出斜率.

易错点

弦长的运算

题型：填空题

填空题 · 5 分

3.在平面直角坐标系中，双曲线的焦距是．

正确答案

；

解析

，因此焦距为．

考查方向

双曲线性质

解题思路

根据双曲线的性质以及求解。

易错点

双曲线中，不要与椭圆中的关系混淆。

知识点

双曲线的定义及标准方程双曲线的几何性质

题型：填空题

填空题 · 5 分

15.已知双曲线过点,且渐近线方程为,则该双曲线的标准方程为．

正确答案

解析

根据双曲线渐近线方程为,可设双曲线的方程为 ,把代入得.所以双曲线的方程为.

考查方向

本题考查双曲线的标准方程，考查学生的计算能力，正确设出双曲线的方程是关键．

解题思路

本题是求双曲线的标准方程,若设标准形式,需先判断焦点是在x轴上,还是在y轴上,而此题解法通过设共渐近线的双曲线的方程,就不需要判断双曲线焦点是在x轴上,还是在y轴上.一般的结论是：以为渐近线的双曲线的方程可设为.

易错点

巧妙设出双曲线方程

知识点

双曲线的定义及标准方程双曲线的几何性质

题型：单选题

单选题 · 5 分

9.将离心率为的双曲线的实半轴长和虚半轴长同时增加个单位

长度，得到离心率为的双曲线，则

A对任意的，

B当时，；当时，

C对任意的，

D当时，；当时，

正确答案

解析

不妨设双曲线的焦点在x轴上，即其方程为：，则双曲线方程为，所以，当时，，所以，同理当可得。

考查方向

1、双曲线的定义；2、双曲线的简单几何性质；

解题思路

分别表示出离心率再去比较大小。

易错点

计算量大计算不出来。

知识点

双曲线的定义及标准方程双曲线的几何性质

题型：填空题

填空题 · 4 分

13．如图，双曲线C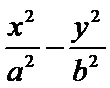：=1（a，b>0）虚轴上的端点B(0，b)，右焦点F，若以B为圆心的圆与C的一条渐近线相切于点P，且BP∥PF，则该双曲线的离心率为．

正确答案

解析

考查方向

本题考查双曲线的离心率，考查学生的计算能力，确定BF垂直于双曲线的渐近线y=x是关键．

解题思路

由题意BF垂直于双曲线的渐近线y=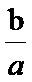x，求出a，c的关系，即可求出该双曲线的离心率．

易错点

垂直的关系应用时候出现问题。

知识点

双曲线的定义及标准方程

题型：单选题

单选题 · 5 分

7．已知双曲线的一条渐近线过点，且双曲线的一个焦点在抛物线的准线上，则双曲线的方程为（）

正确答案

解析

由渐近线过点得，由双曲线的一个焦点在抛物线的准线上得到，再结合；所以选D选项。

考查方向

本题主要考查了求双曲线的方程；属于比较灵活的题，常考求方程、离心率的值或范围、中点弦，面积等问题。

解题思路

1、由渐近线所过的点求出的等量关系；2、焦点在抛物线的准线上得到的值，再由等量关系求出的值；

易错点

本题易在等量关系计算上出问题。

知识点

双曲线的定义及标准方程抛物线的标准方程和几何性质直线、圆及圆锥曲线的交汇问题

题型：填空题

填空题 · 6 分

10．双曲线的实轴长等于，其渐近线与圆相切，则 .

正确答案

6，

解析

试题分析：依题意可知双曲线的标准方程为，故实轴长为6，渐近线方程为，圆的标准方程为，由渐近线与圆相切可得，可解得，故此题答案为6，。

考查方向

本题主要考双曲线的定义、几何性质等知识点．

解题思路

化双曲线方程为标准方程，直接求出实轴长及渐近线方程，利用直线与圆相切即可求出实数m的值。

易错点

知识点

双曲线的定义及标准方程双曲线的几何性质直线、圆及圆锥曲线的交汇问题

题型：单选题

单选题 · 5 分

6．已知双曲线的左顶点与抛物线的焦点的距离为,且双

曲线的一条渐近线与抛物线的准线的交点坐标为,

则双曲线的方程为

正确答案

解析

由已知可得，再由可得a=3，所以只有C答案满足。

考查方向

圆锥曲线的相关计算问题。

解题思路

先画示意图，然后根据双曲线的一条渐近线与抛物线的

准线的交点坐标为,可以将抛物线的方程求出来，再根据已知条件求出

双曲线的方程。

易错点

不会转化为所学内容来做。

知识点

双曲线的定义及标准方程

题型：单选题

单选题 · 5 分

9．设双曲线的右焦点是F，左、右顶点分别是,过F做的垂线与双曲线交于B，C两点，若,则双曲线的渐近线的斜率为（）

正确答案

解析

由已知得右焦点（其中，

，，

从而，又因为，

所以，即，

化简得到，即双曲线的渐近线的斜率为，

故选C.

考查方向

本题考查双曲线的性质，考查斜率的计算，考查学生分析解决问题的能力，比较基础．.

解题思路

本题考查双曲线的简单几何性质，利用向量垂直的条件来转化两直线垂直的条件而得到与的关系式来求解.

易错点

本题属于中档题，注意运算的准确性.

知识点

双曲线的定义及标准方程双曲线的几何性质直线、圆及圆锥曲线的交汇问题

题型：单选题

单选题 · 5 分

5.双曲线（，）的一条渐近线方程为，则的离心率是（）

正确答案

解析

由已知可知，

故选A

考查方向

双曲线的性质，双曲线的渐近线方程

解题思路

根据渐近线方程求出参数的关系，然后求出离心率

易错点

找不到双曲线参数之间的关系

知识点

双曲线的定义及标准方程双曲线的几何性质

继续学习学习下一知识点

下一知识点 : 双曲线的几何性质

百度题库 > 高考 > 文科数学 > 双曲线的定义及标准方程

扫码查看完整答案与解析