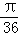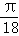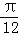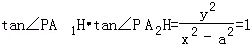- 双曲线的定义及标准方程
- 共193题
已知双曲线



(1)求动点

(2)若








正确答案
见解析。
解析
(1)由题意知:



长轴长为4的椭圆,∴


∴椭圆

(2)由题意,可设直线为:
① 取


直线

若
若点

②以下证明对于任意的




事实上,由


记

设


设



∴


这说明,当


解法二:
(1)同解法一。
(2)取





取








以下证明对于任意的




事实上,由


记



消去

以下用分析法证明
要证明①式恒成立,只需证明
即证

∵
这说明,当


解法三:(1)同解法一,(2)由


记



由
即

这说明,当


知识点
已知A,B,P是双曲线
PA,PB的斜率乘积
正确答案
解析



则

知识点
已知双曲线C:

正确答案
解析
由题意知:

即
知识点
若双曲线

正确答案
8
解析
法一:双曲线的渐近线方程为

由焦点到渐近线的距离为


法二:可以将问题变为“若椭圆

法三:结论法: 在双曲线中,双曲线的焦点到渐近线的距离为b 【在本题中,则b 2=k=(
知识点
双曲线x2﹣y2=2012的左、右顶点分别为A1、A2,P为其右支上一点,且∠A1PA2=4∠PA1A2,则∠PA1A2等于( )
正确答案
解析
解:设P(x,y),y>0,过点P作x轴的垂线PH,垂足为H,
则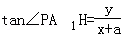
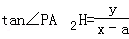
∴
∴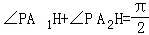
设∠PA1A2=α,则∠PA2H=5α,∴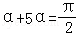
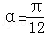
即
知识点
扫码查看完整答案与解析