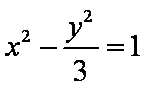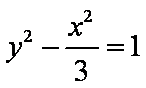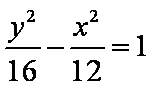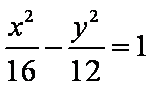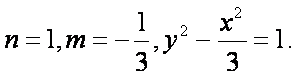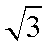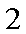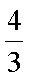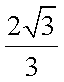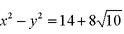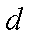双曲线的定义及标准方程
共193题

· 双曲线的定义及标准方程

双曲线的定义及标准方程
共193题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 5 分

已知双曲线中，是左、右顶点，是右焦点，是虚轴的上端点.若在线段上（不含端点）存在不同的两点，使得△构成以为斜边的直角三角形，则双曲线离心率的取值范围是

正确答案

解析

以为直径的圆与线段有两个不同的交点，所以圆的半径大于点到的距离，且小于的长.故，解得.

知识点

双曲线的定义及标准方程

题型：填空题

填空题 · 5 分

过双曲线的右焦点，直平行于经过一、三象限的渐近线的直线方程是　。

正确答案

4x﹣3y﹣20=0

解析

∵双曲线的方程为，

∴a=3，b=4，c=5，故右焦点（5，0）

所以渐进线方程为y=±，

由题意可知所要求的直线斜率为，

故方程为：y﹣0=（x﹣5）

整理可得4x﹣3y﹣20=0

知识点

双曲线的定义及标准方程

题型：单选题

单选题 · 5 分

设双曲线的一个焦点与抛物线的焦点相同，离心率为2，则此双曲线的方程为

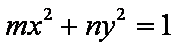
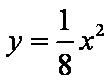
正确答案

解析

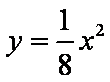
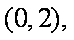
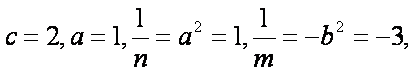
试题分析：因为抛物线的焦点为双曲线离心率为2，所以因此

知识点

双曲线的定义及标准方程

题型：填空题

填空题 · 5 分

过双曲线的右焦点，直平行于经过一、三象限的渐近线的直线方程是　

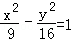
正确答案

4x﹣3y﹣20=0

解析

解：∵双曲线的方程为，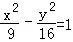

∴a=3，b=4，c=5，故右焦点（5，0）

所以渐进线方程为y=±，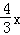

由题意可知所要求的直线斜率为，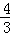

故方程为：y﹣0=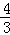（x﹣5）

整理可得4x﹣3y﹣20=0

故答案为：4x﹣3y﹣20=0

知识点

双曲线的定义及标准方程

题型：单选题

单选题 · 5 分

已知是双曲线的两个焦点，以为直径的圆与双曲线一个交点是P，且的三条边长成等差数列，则此双曲线的离心率是

正确答案

解析

略

知识点

双曲线的定义及标准方程

题型：填空题

填空题 · 5 分

已知双曲线C：的一个焦点是抛物线的焦点，且双曲线 C的离心率为，那么双曲线C的方程为____；渐近线方程是____.

正确答案

答案：,

解析

略

知识点

双曲线的定义及标准方程双曲线的几何性质抛物线的标准方程和几何性质

题型：单选题

单选题 · 5 分

已知焦点在x轴的椭圆方程：，过焦点作垂直于x轴的直线交椭圆于A、B两点，且|AB| =1，则该椭圆的离心率为

正确答案

解析

略

知识点

双曲线的定义及标准方程

题型：单选题

单选题 · 5 分

已知双曲线的两条渐近线的夹角为，则双曲线的离心率为

正确答案

解析

略

知识点

双曲线的定义及标准方程

题型：填空题

填空题 · 5 分

已知双曲线的右焦点与抛物线的焦点重合，则该双曲线的焦点到其渐近线的距离为。

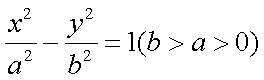
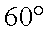
正确答案

解析

试题分析：的焦点，故,渐近线方程,即,焦点到其距离为

知识点

双曲线的定义及标准方程

题型：简答题

简答题 · 12 分

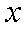
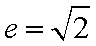
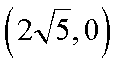
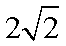
已知双曲线的中心在坐标原点，实轴在轴上，其离心率，已知点到双曲线上的点的最短距离为，求双曲线的方程.

正确答案

或

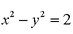
解析

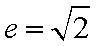
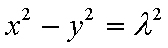
解析：双曲线的其离心率，故双曲线方程可设为……………….2分

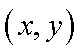
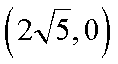
在双曲线上任取一点点到双曲线上的点的距离设为

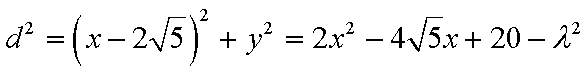
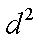
则……………………………….....4分

在区间上的最小值为8………………………………………………6分

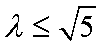
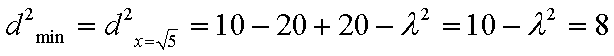
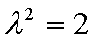
当时，，解得；….8分

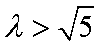
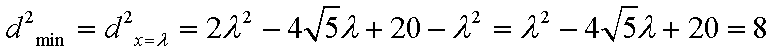
当时，，

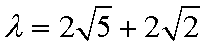
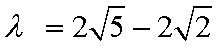
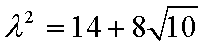
解得或（舍），即；……10分

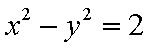
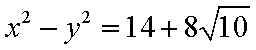
综上：双曲线的方程为或……………………………12分

知识点

双曲线的定义及标准方程

继续学习学习下一知识点

下一知识点 : 双曲线的几何性质

百度题库 > 高考 > 文科数学 > 双曲线的定义及标准方程

扫码查看完整答案与解析