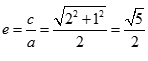• 职业资格类
  • 建筑类
  • 学历类
  • 财会类
  • 医药类
  • 全部考试
职业资格类
建筑类
学历类
财会类
计算机类
公务员
医药类
  • 双曲线的定义及标准方程
  • 共193题
  • 双曲线的定义及标准方程
  • 共193题

热门试卷

X 查看更多试卷
1
题型：填空题
|
填空题 · 5 分

双曲线的左、右焦点分别为和，左、右顶点分别为和，过焦点与轴垂直的直线和双曲线的一个交点为，若是和的等差中项，则该双曲线的离心率为          

正确答案

2

解析

由题可知，则，化简得，故.

知识点

双曲线的定义及标准方程
1
题型：简答题
|
简答题 · 12 分

已知曲线的方程为，曲线是以、为焦点的椭圆，点为曲线与曲线在第一象限的交点，且。

（1）求曲线的标准方程；

（2）直线与椭圆相交于，两点，若的中点在曲线上，求直线的斜率的取值范围。

正确答案

（1）（2）

解析

（1）依题意，，,利用抛物线的定义可得，

点的 坐标为…………………2分

,又由椭圆定义得.………………4分

，所以曲线的标准方程为； …………………6分

（2）（方法一）设直线与椭圆交点，的中点的坐标为，

设直线方程为

与联立得

由①    …………………8分

由韦达定理得      

将M(,)代入 整理得②……………10分

将②代入①得

令则

且 …………………12分

（方法二）设直线与椭圆交点，的中点的坐标为，

将的坐标代入椭圆方程中，得

两式相减得

， …………………7分

，直线的斜率，  …………………8分

由，

，解得，或（舍）

由题设，，………………10分

即.  …………………12分

知识点

双曲线的定义及标准方程
1
题型：填空题
|
填空题 · 4 分

14.如图所示，为双曲线的左焦点，双曲线上的点与关于轴对称，则的值是           ．

正确答案

48

解析

设右焦点为，则,所以

==6a=48

知识点

双曲线的定义及标准方程
1
题型：填空题
|
填空题 · 5 分

10.已知双曲线﹣=1（a＞0，b＞0）的一条渐近线垂直于直线l：x﹣2y﹣5=0，双曲线的一个焦点在l上，则双曲线的方程为（）

正确答案

=1.

解析

∵双曲线的一个焦点在直线l上，

令y=0，可得x=5，即焦点坐标为（5，0），∴c=5，

∵双曲线﹣=1（a＞0，b＞0）的一条渐近线垂直于直线l：x﹣2y﹣5=0，

∴=2，∵c2=a2+b2，∴a2=5，b2=20，

∴双曲线的方程为=1.故答案为：=1.

知识点

双曲线的定义及标准方程
1
题型：填空题
|
填空题 · 5 分

设F1、F2是双曲线的两焦点，点P在双曲线上，若点P到焦点F1的距离等于9，则点P到焦点F2的距离等于             。

正确答案

1或17

解析

由双曲线的定义知：，即点P到焦点F2的距离等于1或17。

知识点

双曲线的定义及标准方程
1
题型：简答题
|
简答题 · 13 分

已知圆锥曲线的两个焦点坐标是，且离心率为；

（1）求曲线的方程；

（2）设曲线表示曲线的轴左边部分，若直线与曲线相交于两点，求的取值范围；

（3）在条件（2）下，如果，且曲线上存在点，使，求的值。

正确答案

（1）

（2）

（3）m=4

解析

（1）由知，曲线是以为焦点的双曲线，且，

故双曲线的方程是， 

（2）设，联立方程组：，

从而有：为所求。  

（3）因为，

整理得或，

注意到，所以，故直线的方程为。

设，由已知，

又，所以。

在曲线上，得，

但当时，所得的点在双曲线的右支上，不合题意，

所以为所求。                       

知识点

向量在几何中的应用双曲线的定义及标准方程双曲线的几何性质直线与圆锥曲线的综合问题圆锥曲线中的范围、最值问题
1
题型：填空题
|
填空题 · 4 分

已知双曲线kx2-y2=1的一条渐近线与直线2x+y+1=0垂直，那么双曲线的离心率为_________。

正确答案

解析

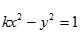
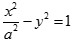
设双曲线为，它的一条渐近线方程为

直线2x+y+1=0的斜率为-2

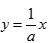
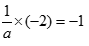
∵直线与直线2x+y+1=0垂直，

∴   即a=2

∴

知识点

双曲线的定义及标准方程
1
题型： 单选题
|
单选题 · 5 分

7.已知双曲线﹣  =1（a＞0）的离心率为2，则a=（　　）

A2

B

C

D1

正确答案

D

解析

双曲线的离心率e==2，解答a=1，故选D。

知识点

双曲线的定义及标准方程
1
题型： 单选题
|
单选题 · 5 分

9.已知F1，F2是双曲线的两焦点，以线段F1F2为边作正三角形MF1F2，若边MF1的中点在双曲线上，则双曲线的离心率是（　　）

A4+2

B﹣1

C

D

正确答案

D

解析

依题意可知双曲线的焦点为F1（﹣c，0），F2（c，0）

∴F1F2=2c∴三角形高是cM（0，c）所以中点N（﹣，c）

代入双曲线方程得：=1整理得：b2c2﹣3a2c2=4a2b2∵b2=c2﹣a2

所以c4﹣a2c2﹣3a2c2=4a2c2﹣4a4整理得e4﹣8e2+4=0求得e2=4±2∵e＞1，

∴e=+1故选D。

知识点

双曲线的定义及标准方程
1
题型：填空题
|
填空题 · 5 分

13.若双曲线E的标准方程是，则双曲线E的渐进线的方程是　    　．

正确答案

y=x

解析

双曲线E的标准方程是，

则a=2，b=1，

即有渐近线方程为y=x，

即为y=x．

故答案为：y=x．

知识点

双曲线的定义及标准方程
继续学习 学习下一知识点
下一知识点 : 双曲线的几何性质
百度题库 > 高考 > 文科数学 > 双曲线的定义及标准方程

扫码查看完整答案与解析

  • 上一题
  • 1/10
  • 下一题