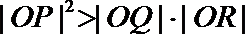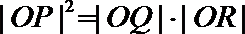- 双曲线的定义及标准方程
- 共193题
11.已知双曲线中心在原点,一个焦点为



正确答案
解析
略
知识点
17.若直线


正确答案
{1,-1,

解析
当
当

知识点
11. 已知双曲线


正确答案
解析
略
知识点
13.设双曲线


正确答案
解析
略。
知识点
18.在△ABC中(如图1),已知AC=BC=2,∠ACB=120°,D,E,F分别为AB,AC,BC的中点,EF交CD于G,把△ADC沿CD折成如图2所示的三棱锥C﹣A1BD.
(1)求证:E1F∥平面A1BD;
(2)若二面角A1﹣CD﹣B为直二面角,求直线A1F与平面BCD所成的角.
正确答案
见解析。
解析
(1)证明:E1,F分别为AC,BC的中点,
则E1F为A1BC的中位线,
故E1F∥A1B
因为A1B⊂面A1BD,E1F⊄平面A1BD,
所以E1F∥平面A1BD.
(2)连结DF,∵二面角A1﹣CD﹣B为直二面角,
∴A1D⊥BD,
又∵AC=BC且D为AB的中点,∴A1D⊥CD,
得A1D⊥平面BDC,
故∠A1FD为直线A1F与平面BCD所成的角
在△ABC中,AC=BC=2,∠ACB=120°,
得CD=1,CF=1,∠DCF=60°
∴△CDF为等边三角形,
故DF=1,
则
故直线A1F与平面BCD所成的角为60°.
知识点
17.若直线


正确答案
解析
当
当
知识点
12.设双曲线





正确答案
解析
双曲线的渐近线为:y=±



∵


∴λ+μ=1,λ﹣μ=


又由λμ=




∴e=
故选C.
知识点
12.若双曲线


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5. 已知双曲线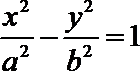
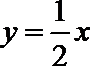
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.设双曲线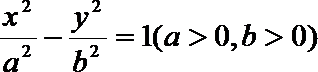
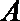
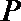
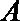
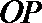
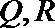
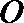
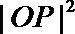

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析