- 定积分
- 共55题
设函数
(1)若曲线



(2)求函数
正确答案
(1)a=4,b =24
(2)



解析
(1)
∵曲线


∴
(2)∵
当



此时函数
当

当


当


当


∴此时



知识点
统计表明,某种型号的汽车在匀速行驶中每小时耗油量y(升)关于行驶速度x(千米/小时)的函数解析式可以表示为:
(1)当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(2)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
正确答案
(1)17.5升
(2)当汽车以80千米/小时的速度匀速行驶时,耗油最少,最少为11.25升
解析
(1)当x=40时,汽车从甲地到乙地行驶了=2.5小时,
要耗油(×403-×40+8)×2.5=17.5(升)。
所以,当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地耗油17.5.
(1)当速度为x千米/小时时,汽车从甲地到乙地
依题意得h(x)=(x3-x+8)·=x2+-(0<x≤120),
h`(x)=
当x∈(0,80)时,

∴当x=80时,h(x)取到极小值h(80)=11.25,因为h(x)在(0,120]上只有一个极值,所以它是最小值。
故当汽车以80千米/小时的速度匀速行驶时,从甲地到乙地耗油最少,最少为11.25升。
知识点
设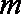
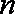
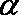
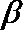

(1)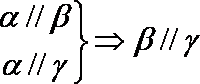
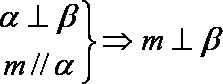
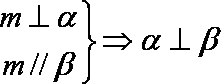
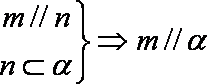
正确答案
解析
根据面面平行的性质可知,(1)正确,排除C,D,根据线面垂直的性质,可知(3)正确,所以选B.
知识点
已知函数
(1)
(2)设h(x)= f(x)+ g(x),且h(x)有两个极值点为x1 , x2 ,其中
正确答案
(1)
解析
(1)由题意


对于

①当



②当


∴




综上:当


当





(2)对

求导得,
由题




∴


当



又
∴
知识点
执行如图所示的程序框图,若输入

正确答案
解析
略
知识点
扫码查看完整答案与解析







