直线与抛物线的位置关系
共49题

· 直线与抛物线的位置关系

直线与抛物线的位置关系
共49题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

8．已知定义域为的函数满足，则时，单调递增，若，且，则与0的大小关系是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

直线与抛物线的位置关系

题型：单选题

单选题 · 5 分

设关于x，y的不等式组表示的平面区域内存在点P(x0，y0)，满足x0－2y0＝2，求得m的取值范围是(　　)。

正确答案

解析

图中阴影部分表示可行域，要求可行域内包含y＝x－1上的点，只需要可行域的边界点(－m，m)在y＝x－1下方，也就是m＜m－1，即.故选C.

知识点

直线与抛物线的位置关系

题型：填空题

填空题 · 4 分

设为抛物线的焦点，过点的直线交抛物线于两点，点为线段的中点，若，则直线的斜率等于________。

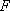
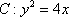
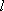
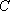
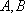
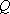
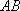
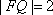
正确答案

解析

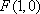
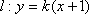
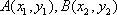
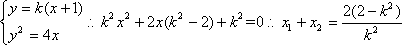
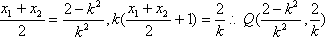
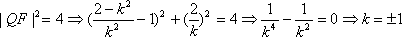
由已知得到：，设，，由，所以

，由已知得到

，所以答案是

知识点

抛物线的标准方程和几何性质直线与抛物线的位置关系

题型：单选题

单选题 · 5 分

直线截圆所得劣弧所对的圆心角是

正确答案

解析

略

知识点

直线与抛物线的位置关系

题型：简答题

简答题 · 12 分

已知函数满足如下条件：当时，，且对任意，都有。

（1）求函数的图象在点处的切线方程；

（2）求当，时，函数的解析式；

（3）是否存在，，使得等式

成立？若存在就求出（），若不存在，说明理由。

正确答案

见解析。

解析

（1）时，，，

所以，函数的图象在点处的切线方程为

，即。

（2）因为，

所以，当，时，，

。

（3）考虑函数，，，

则，

当时，，单调递减；

当时，；

当时，，单调递增；

所以，当，时，，

当且仅当时，。

所以，

而，

令，则，

两式相减得，

。

所以，，

故。

所以，。

当且仅当时，

。

所以，存在唯一一组实数，，

使得等式成立。

知识点

直线与抛物线的位置关系

继续学习棒棒哒，已是最后一个知识点

已完结

百度题库 > 高考 > 理科数学 > 直线与抛物线的位置关系

扫码查看完整答案与解析